Supermarket
Time Limit:2000MS Memory Limit:65536K
Total Submit:987 Accepted:369
Description
A supermarket has a set Prod of products on sale. It earns a profit px for each product x∈Prod sold by a deadline dx that is measured as an integral number of time units starting from the moment the sale begins. Each product takes precisely one unit of time for being sold. A selling schedule is an ordered subset of products Sell ≤ Prod such that the selling of each product x∈Sell, according to the ordering of Sell, completes before the deadline dx or just when dx expires. The profit of the selling schedule is Profit(Sell)=Σx∈Sellpx. An optimal selling schedule is a schedule with a maximum profit.
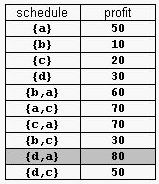
For example, consider the products Prod={a,b,c,d} with (pa,da)=(50,2), (pb,db)=(10,1), (pc,dc)=(20,2), and (pd,dd)=(30,1). The possible selling schedules are listed in table 1. For instance, the schedule Sell={d,a} shows that the selling of product d starts at time 0 and ends at time 1, while the selling of product a starts at time 1 and ends at time 2. Each of these products is sold by its deadline. Sell is the optimal schedule and its profit is 80.
Write a program that reads sets of products from an input text file and computes the profit of an optimal selling schedule for each set of products.
Input
A set of products starts with an integer 0 <= n <= 10000, which is the number of products in the set, and continues with n pairs pi di of integers, 1 <= pi <= 10000 and 1 <= di <= 10000, that designate the profit and the selling deadline of the i-th product. White spaces can occur freely in input. Input data terminate with an end of file and are guaranteed correct.
Output
For each set of products, the program prints on the standard output the profit of an optimal selling schedule for the set. Each result is printed from the beginning of a separate line.
Sample Input
4 50 2 10 1 20 2 30 1
7 20 1 2 1 10 3 100 2 8 2
5 20 50 10
Sample Output
80
185
Hint
The sample input contains two product sets. The first set encodes the products from table 1. The second set is for 7 products. The profit of an optimal schedule for these products is 185.
Source
Southeastern Europe 2003
贪心是很容易想到的 尽可能将利润大的选中 然后尽可能放到DeadLine附近去
这里就有一个问题 怎样尽快拿到一个deadLine往上数第一个空闲日期?
想法0:直接搜o(n^2)的查找总费时 可能超时!
想法1:线段树!问题建模:一个数的前面第几个是空闲?
对10000的区间建立线段树 可以将查询复杂度降低到NlogN
想法2: 并查集!对一个连续非空闲区间建立集合 其代表元选择上面第一个空闲的日期!时间复杂度再降低到o(N)! 系数为ackman函数 很小
Problem Id:1456 User Id:oyjpart
Memory:172K Time:15MS
Language:G++ Result:Accepted
//by oyjpArt
#include <stdio.h>
#include <string.h>
#include <algorithm>
using namespace std;
const int N = 10010;
int ng;
struct good{int p, d;}g[N];
int p[N];
bool flag[N];
bool operator < (const good& a, const good& b) {return a.p > b.p; }
int find_set(int a) {
int t = a;
while(t != p[t]) t = p[t];
int r = a;
while(r != p[r]) { int k = p[r]; p[r] = t; r = k; }
return t;
}
int main() {
int i;
while(scanf("%d", &ng) != EOF) {
memset(flag, 0, sizeof(flag));
int maxd = 0;
for(i = 0; i<ng; i++) {
scanf("%d%d", &(g[i].p), &(g[i].d));
if(g[i].d > maxd) maxd = g[i].d;
}
for(i = 1; i<maxd; i++)
p[i] = i;
sort(g, g+ng);
int cnt = 0;
for(i = 0; i<ng; i++) {
int d;
if(!flag[g[i].d]) { d = g[i].d; p[d] = d-1; }
else d = find_set(g[i].d);
if(d > 0) cnt += g[i].p;
flag[d] = 1;
if(d > 0 && flag[d+1]) p[d] = p[d-1];
}
printf("%d\n", cnt);
}
return 0;
}