Radar Installation
Time Limit:1000MS Memory Limit:10000K
Total Submit:2704 Accepted:564
Description
Assume the coasting is an infinite straight line. Land is in one side of coasting, sea in the other. Each small island is a point locating in the sea side. And any radar installation, locating on the coasting, can only cover d distance, so an island in the sea can be covered by a radius installation, if the distance between them is at most d.
We use Cartesian coordinate system, defining the coasting is the x-axis. The sea side is above x-axis, and the land side below. Given the position of each island in the sea, and given the distance of the coverage of the radar installation, your task is to write a program to find the minimal number of radar installations to cover all the islands. Note that the position of an island is represented by its x-y coordinates.
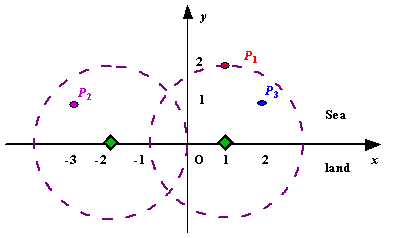
Figure A Sample Input of Radar Installations
Input
The input consists of several test cases. The first line of each case contains two integers n (1<=n<=1000) and d, where n is the number of islands in the sea and d is the distance of coverage of the radar installation. This is followed by n lines each containing two integers representing the coordinate of the position of each island. Then a blank line follows to separate the cases.
The input is terminated by a line containing pair of zeros
Output
For each test case output one line consisting of the test case number followed by the minimal number of radar installations needed. "-1" installation means no solution for that case.
Sample Input
3 2
1 2
-3 1
2 1
1 2
0 2
0 0
Sample Output
Case 1: 2
Case 2: 1
Source
Beijing 2002
Algorithm: Greedy
Step 1: 输入数据 如果有一个点的y坐标大于d 直接输出-1 长生相应的区间(在某一个区间里任意放置一个Radar 则是这个Island可视)
Step 2: 按照左端点排序(如果左端点相等 则必须按右边反向排序, 理由在于下一步为了筛选出包含的 必须的把大范围的放到前面) 注意这里面最好要用浮点判断规则
Step 3: 利用Stack对这些区间做预处理 把被包含的区间标识出来
Step 4: 贪心选择右端的点
#include <stdio.h>
#include <string.h>
#include <algorithm>
#include <math.h>
using namespace std;
const int N = 1000;
const double EPS = 1e-7;
struct E { double a, b; } e[N];
int n, d;
bool ava[N];
double p[N];
inline int dblcmp(double a, double b) {
if( fabs(a-b) < EPS ) return 0;
if( a-b > 0 ) return 1;
return -1;
}
bool operator<(const E& a, const E& b) {
if(dblcmp(a.a, b.a) == 0)
return dblcmp(a.b, b.b) == 1;
return dblcmp(a.a, b.a) == -1;
}
int main() {
int i, j, x, y;
int tc = 0;
while(scanf("%d %d", &n, &d), n + d) {
tc++;
int ok = 1;
for(i = 0; i < n; ++i) {
scanf("%d %d", &x, &y);
if(y > d) ok = 0;
double offset = sqrt ( d * d - y * y );
e[i].a = x - offset, e[i].b = x + offset;
ava[i] = 1;
}
if(!ok) { printf("Case %d: -1\n", tc); continue; }
sort(e, e + n);
int stack[N], top = 0;
stack[top++] = 0;
for(i = 1; i < n; ++i) {
while(top > 0 && dblcmp(e[stack[top-1]].b, e[i].b) != -1) {
ava[stack[--top]] = 0;
}
stack[top++] = i;
}
for(i = 0; !ava[i]; ++i);
p[i] = e[i].b;
int cnt = 1;
for(i = i+1; i < n; ++i) if(ava[i]) {
for(j = i-1; !ava[j]; j--);
if(p[j] >= e[i].a) p[i] = p[j];
else { p[i] = e[i].b; cnt++; }
}
printf("Case %d: %d\n", tc, cnt);
}
return 0;
}