It makes use of the fact that the transpose graph (the same graph with the direction of every edge reversed) has exactly the same strongly connected components as the original graph.
它利用了有向图的这样一个性质,一个图和他的transpose graph(边全部反向)具有相同的强连通分量!
算法伪代码
Kosaraju's algorithm is simple and works as follows:
- Let G be a directed graph and S be an empty stack.
- While S does not contain all vertices:
- Choose an arbitrary vertex v not in S. Perform a depth-first search starting at v. Each time that depth-first search finishes expanding a vertex u, push u onto S.
- Reverse the directions of all arcs to obtain the transpose graph.
- While S is nonempty:
- Pop the top vertex v from S. Perform a depth-first search starting at v. The set of visited vertices will give the strongly connected component containing v; record this and remove all these vertices from the graph G and the stack S. Equivalently,breadth-first search (BFS) can be used instead of depth-first search.
需要注意的是这里的第一遍BFS搜索的时候的入队序列,Each time that depth-first search finishes expanding a vertex u, push u onto S.只有当扩展结束了此节点之后,此节点才会被push onto S.
算法思路:
1, 后序遍历原图,对每个访问到的节点标记时间戳。
2, 按照时间戳的降序遍历反向图,得到的每个连通块就是一个强连通分量。
证明是很简单的:
假设以上算法从u访问到了v,那么说明反向图有一条从u到v的边,也就说明了原图中有一条从v到u的边,又因为u的标号是大于v的,那么,u一定在v之前访问到(否则v的标号将大于u),并且是从u访问到v了的(v到u也有一条路径,否则就会从v访问到u)。
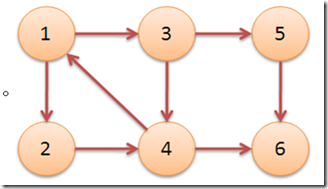
如果应用我们第一个Tarjan算法的例子的话,第一遍DFS 得到的次序是 6 4 2 5 3 1
代码
#include "cstdlib"
#include "cctype"
#include "cstring"
#include "cstdio"
#include "cmath"
#include "algorithm"
#include "vector"
#include "string"
#include "iostream"
#include "sstream"
#include "set"
#include "queue"
#include "stack"
#include "fstream"
#include "strstream"
using namespace std;
#define M 2000
bool vis[M]; //遍历数组
int post[M]; //时间戳对应的点
int timestamp; //时间戳
int ComponetNumber=0; //有向图强连通分量个数
vector <int> Edge[M]; //邻接表表示
vector <int> Opp[M]; //原图的反图
vector <int> Component[M]; //获得强连通分量结果
void dfs(int u) { //第一个dfs确定时间戳
vis[u] = true;
for(int i=0;i<Edge[u].size();i++) {
if(vis[ Edge[u][i]]) continue;
//cout<<Edge[u][i]<<endl;
dfs(Edge[u][i]);
}
//cout<<"timestamp "<<timestamp<<" "<<u<<endl;
post[timestamp++] = u;
}
void dfs2(int u) { //第二个反边dfs确定连通块
vis[u] = true;
Component[ComponetNumber].push_back(u);
for(int i=0;i<Opp[u].size();i++)
{
int v = Opp[u][i];
if(vis[v]) continue;
dfs2(v);
}
}
void Kosaraju(int n) {
memset(vis,0,sizeof(vis));
timestamp = 0;
for(int i=0;i<n;i++) {
if(vis[i]) continue;
dfs(i);
}
memset(vis,0,sizeof(vis));
ComponetNumber++;
for(int i=n-1;i>=0;i--) {//按时间戳从大到小搜
if(vis[post[i]]) continue;
Component[ComponetNumber].clear();
dfs2(post[i]);
ComponetNumber++;
}
ComponetNumber--; //最后我们把块加了1。。所以要减掉
}
int main()
{
Edge[0].push_back(1);Edge[0].push_back(2);
Edge[1].push_back(3);
Edge[2].push_back(3);Edge[2].push_back(4);
Edge[3].push_back(0);Edge[3].push_back(5);
Edge[4].push_back(5);
Opp[0].push_back(3);
Opp[1].push_back(0);
Opp[2].push_back(0);
Opp[3].push_back(1);Opp[3].push_back(2);
Opp[4].push_back(2);
Opp[5].push_back(3);Opp[6].push_back(4);
int N=6;
Kosaraju(N);
cout<<"ComponetNumber is "<<ComponetNumber<<endl;
for(int i=0;i<N;i++)
{
for(int j=0;j<Component[i].size();j++)
cout<<Component[i][j];
cout<<endl;
}
return 0;
}
此算法的时间复杂度当然也是 O(M+N)(M条边,N个点)与Tarjan算法相似。。但是在系数上不如Tarjan算法!在实际的测试中,Tarjan算法的运行效率也比Kosaraju算法高30%左右。
当然Kosaraju算法额外花费的时间,也不是白费的,它获得了图的一个拓扑性质哦!!
如果我们把求出来的每个强连通分量收缩成一个点,并且用求出每个强连通分量的顺序来标记收缩后的节点,那么这个顺序其 实就是强连通分量收缩成点后形成的有向无环图的拓扑序列。为什么呢?首先,应该明确搜索后的图一定是有向无环图呢?废话,如果还有环,那么环上的顶点对应 的所有原来图上的顶点构成一个强连通分量,而不是构成环上那么多点对应的独自的强连通分量了。然后就是为什么是拓扑序列,我们在改进分析的时候,不是先选 的树不会连通到其他树上(对于反图GT来说),也就是后选的树没有连通到先选的树,也即先出现的强连通分量收缩的点只能指向后出现的强连通分量收缩的点。那么拓扑序列不是理所当然的吗?这就是Kosaraju算法的一个隐藏性质。
Reference :
http://www.notonlysuccess.com/?p=181
推荐一下啊!终于算是搞的差不多了。。下面就是做一些练习,然后巩固提高一下!接下来剩下的最后一个算法了:Gabow 算法