贝叶斯定理在数据挖掘,邮件过滤,人工智能方面都有应用,近几年来开始被广泛关注

当另一事件B发生时,事件A的条件概率是
Pr{A|B}=Pr{A&B}/Pr{B}
另外
Pr{B|A}=Pr{A&b}/Pr{A}
===>Pr{A|B} Pr{B}= Pr{B|A}Pr{A}
===>Pr{A|B}= Pr{B|A}Pr{A}/Pr{B}
又
Pr{B}=Pr{A&B}+Pr{~A&B}
===>Pr{A|B}=Pr{B|A}Pr{A}/(Pr{A&B}+Pr{~A&B})=Pr{B|A}Pr{A}/(Pr{B|A}Pr{A}+Pr{B|~A}Pr{~A})
===>Pr{A|B}= Pr{B|A}Pr{A}/(Pr{B|A}Pr{A}+Pr{B|~A}Pr{~A})
Bayes network
贝叶斯网络(Bayesian Network)贝叶斯网络是一种基于网络结构的有向图解描述,是用来表示变量集合连接概率的图形模型,适用于表达和分析不确定和概率性事物,可从不完全或不确定的知识或信息中作出推理。一个贝叶斯网络是一个有向无环图(Directed Acyclic Graph, DAG),由代表变量节点及连接这些节点有向边构成。节点代表随机变量,节点间的有向边代表了节点间的相互关系(由父节点指向其后代节点),用条件概率进行表达关系强度,没有父节点的用先验概率进行信息表达。节点变量可以是任何问题的抽象,如测试值、观测现象、意见征询等。
贝叶斯因果网公式
P(x)=P(Vi|Vp)
Vp为所有Vi的双亲结点,根据具体的关系可减少Vp中的特定结点,只留下邻结点。
例子:
A--->B--->C
P(A,B,C)=P(A)*P(B|A)*P(C|A,B)= P(A)*P(B|A)*P(C|B)
通常网路上资料都举一个草地变湿的例子,有的加上了云形成的概率,简单起见。
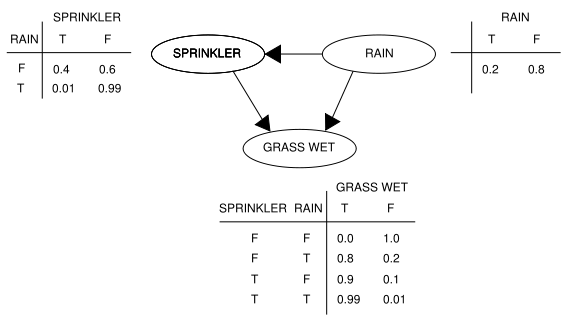
R=RAIN S=SPPRINKLER G=GRASS WET
假设草地湿了,那么有可能是洒水车或下雨造成。那么由于下雨造成的可能性这样计算(数据查表可知)
P(R|G)=P(R,G)/P(G)=(0.2*0.8*0.99+0.2*0.99*0.11)/(0.8*0.2*0.99+0.9*0.8*0.4+0.99*0.2*0.01)=35.77%
其余也可一次计算。
贝叶斯在邮件过滤方面的算法打算研究一下,呵呵。过几天再看吧。
相关的链接
http://en.wikipedia.org/wiki/Bayes'_theorem
http://www.cim.mcgill.ca/~friggi/bayes/