此题看了官方标程,才知道怎么做,其解法实在是相当巧妙!
数据给出的点是顺时针顺序的,这点非常重要,我们可以根据这个整理出每条线段的方向。
我们可以发现这个规律:
对于某一列格子,在遇到第一条线段之前,一定是空白的,在第一条线段与第二条线段之间,一定是填充的。。以此类推。
而且经过这一列格子的线段数一定是偶数。
标程给出的算法是:
开一个二维数组保存每个格子黑色部分的面积。
如果这个线段是从左到右的,那么就给这条线段以上的格子加上一个负的面积。
如果是从右到左的,则加上一个正的面积。
如果是垂直的,则忽略这条线段。
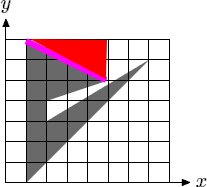
比如说第一条线段是从左到右的,在它以上一共有5个格子,面积依次为:-0.3 -0.6 -1.0 -1.0 -0.6 (大概的数字)
第二条线段是从右到左的,在它以上一共有9个格子,面积依次为:1.0 1.0 1.0 1.0 1.0 1.0 0.6 0.5 0.3
第三条线段是垂直的,忽略它。
第四条线段是从左到右的,在它以上一共有16个格子。。(其中有一个很小很小的)
等等。
给这些格子加上或正或负的增量之后,会发现,恰好完全空白的地方的面积都是0,都被抵消了。
而部分黑色的格子,它的值也是正确的。这就是这个算法的神奇之处~
标程在这里
{$APPTYPE CONSOLE}
{$R+,Q+,S+,H+,O-}
uses
Math, SysUtils;
Type
Integer=LongInt;
Real=Extended;
Const
TaskID='ascii';
InFile=TaskID+'.in';
OutFile=TaskID+'.out';
MaxN=100;
MaxSize=100;
Eps=1e-12;
Var
N,W,H:Integer;
X,Y:Array[1..MaxN]Of Integer;
Res:Array[-1..MaxSize,-1..MaxSize]Of Real;
Procedure Load;
Var
I:Integer;
Begin
ReSet(Input,InFile);
Read(N,W,H);
For I:=1 To N Do Read(X[I],Y[I]);
Close(Input);
End;
Function Floor(A:Real):Integer;
Begin
Result:=Trunc(A+1000)-1000;
End;
Function Ceil(A:Real):Integer;
Begin
Result:=-Floor(-A);
End;
Procedure Process(X1,Y1,X2,Y2,By:Integer);
Var
I,X,Y,U,D:Integer;
XU,XD,YL,YR,Tmp:Real;
Begin
For X:=X1 To X2-1 Do Begin
YL:=(X-X1)/(X2-X1)*(Y2-Y1)+Y1;
YR:=((X+1)-X1)/(X2-X1)*(Y2-Y1)+Y1;
If YL<YR Then Begin
For I:=0 To Floor(YL)-1 Do Res[X,I]:=Res[X,I]+By;
D:=Floor(YL);
U:=Ceil(YR)-1;
If D=U Then Begin
Res[X,D]:=Res[X,D]+By*(YL-D+YR-D)/2;
End Else If D<U Then Begin
XU:=(D+1-Y1)/(Y2-Y1)*(X2-X1)+X1;
Res[X,D]:=Res[X,D]+By*(1-(XU-X)*(D+1-YL)/2);
XD:=(U-Y1)/(Y2-Y1)*(X2-X1)+X1;
Res[X,U]:=Res[X,U]+By*((YR-U)*(X+1-XD)/2);
For I:=D+1 To U-1 Do Begin
XU:=(I+1-Y1)/(Y2-Y1)*(X2-X1)+X1;
XD:=(I-Y1)/(Y2-Y1)*(X2-X1)+X1;
Res[X,I]:=Res[X,I]+By*(X+1-XD+X+1-XU)/2;
End;
End;
End Else Begin
For I:=0 To Floor(YR)-1 Do Res[X,I]:=Res[X,I]+By;
D:=Floor(YR);
U:=Ceil(YL)-1;
If D=U Then Begin
Res[X,D]:=Res[X,D]+By*(YL-D+YR-D)/2;
End Else If D<U Then Begin
XU:=(D+1-Y1)/(Y2-Y1)*(X2-X1)+X1;
Res[X,D]:=Res[X,D]+By*(1-(X+1-XU)*(D+1-YR)/2);
XD:=(U-Y1)/(Y2-Y1)*(X2-X1)+X1;
Res[X,U]:=Res[X,U]+By*((YL-U)*(XD-X)/2);
For I:=D+1 To U-1 Do Begin
XU:=(I+1-Y1)/(Y2-Y1)*(X2-X1)+X1;
XD:=(I-Y1)/(Y2-Y1)*(X2-X1)+X1;
Res[X,I]:=Res[X,I]+By*(XD-X+XU-X)/2;
End;
End;
End;
End;
End;
Procedure Solve;
Var
I,X1,Y1,X2,Y2:Integer;
Begin
FillChar(Res,SizeOf(Res),0);
For I:=1 To N Do Begin
X1:=X[I];
Y1:=Y[I];
X2:=X[I Mod N+1];
Y2:=Y[I Mod N+1];
If X1=X2 Then Continue;
If X1<X2 Then
Process(X1,Y1,X2,Y2,1)
Else
Process(X2,Y2,X1,Y1,-1);
End;
End;
Procedure Save;
Var
X,Y:Integer;
R:Real;
Begin
ReWrite(Output,OutFile);
For Y:=H-1 DownTo 0 Do Begin
For X:=0 To W-1 Do Begin
R:=Res[X,Y];
If R<1/4-Eps Then Write('.') Else If R<1/2-Eps Then Write('+') Else If R<3/4-Eps Then Write('o') Else If R<1-Eps Then Write('$') Else Write('#');
End;
WriteLn;
End;
Close(Output);
End;
begin
Load;
Solve;
Save;
end.