Dijkstra(迪杰斯特拉)算法是典型的最短路径路由算法，用于计算一个节点到其他所有节点的最短路径。主要特点是以起始点为中心向外层层扩展，直到扩展到终点为止。Dijkstra算法能得出最短路径的最优解，但由于它遍历计算的节点很多，所以效率低。

Dijkstra算法是很有代表性的最短路算法，在很多专业课程中都作为基本内容有详细的介绍，如数据结构，图论，运筹学等等。

其基本思想是，设置顶点集合S并不断地作贪心选择来扩充这个集合。一个顶点属于集合S当且仅当从源到该顶点的最短路径长度已知。

初始时，S中仅含有源。设u是G的某一个顶点，把从源到u且中间只经过S中顶点的路称为从源到u的特殊路径，并用数组dist记录当前每个顶点所对应的最短特殊路径长度。Dijkstra算法每次从V-S中取出具有最短特殊路长度的顶点u，将u添加到S中，同时对数组dist作必要的修改。一旦S包含了所有V中顶点，dist就记录了从源到所有其它顶点之间的最短路径长度。

例如，对下图中的有向图，应用Dijkstra算法计算从源顶点1到其它顶点间最短路径的过程列在下表中。

Dijkstra算法的迭代过程：

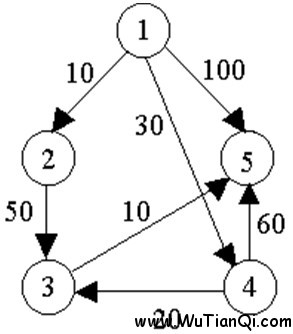
主题好好理解上图！

以下是具体的实现(C/C++):

  1 #include <iostream>
  2 using namespace std;
  3
  4 const int maxnum = 100;
  5 const int maxint = 999999;
  6
  7 // 各数组都从下标1开始
  8 int dist[maxnum];     // 表示当前点到源点的最短路径长度
  9 int prev[maxnum];     // 记录当前点的前一个结点
10 int c[maxnum][maxnum];   // 记录图的两点间路径长度
11 int n, line;             // 图的结点数和路径数
12
13 // n -- n nodes
14 // v -- the source node
15 // dist[] -- the distance from the ith node to the source node
16 // prev[] -- the previous node of the ith node
17 // c[][] -- every two nodes' distance
18 void Dijkstra(int n, int v, int *dist, int *prev, int c[maxnum][maxnum])
19 {
20     bool s[maxnum];    // 判断是否已存入该点到S集合中
21     for(int i=1; i<=n; ++i)
22     {
23         dist[i] = c[v][i];
24         s[i] = 0;     // 初始都未用过该点
25         if(dist[i] == maxint)
26             prev[i] = 0;
27         else
28             prev[i] = v;
29     }
30     dist[v] = 0;
31     s[v] = 1;
32
33     // 依次将未放入S集合的结点中，取dist[]最小值的结点，放入结合S中
34     // 一旦S包含了所有V中顶点，dist就记录了从源点到所有其他顶点之间的最短路径长度
35          // 注意是从第二个节点开始，第一个为源点
36     for(int i=2; i<=n; ++i)
37     {
38         int tmp = maxint;
39         int u = v;
40         // 找出当前未使用的点j的dist[j]最小值
41         for(int j=1; j<=n; ++j)
42             if((!s[j]) && dist[j]<tmp)
43             {
44                 u = j;              // u保存当前邻接点中距离最小的点的号码
45                 tmp = dist[j];
46             }
47         s[u] = 1;    // 表示u点已存入S集合中
48
49         // 更新dist
50         for(int j=1; j<=n; ++j)
51             if((!s[j]) && c[u][j]<maxint)
52             {
53                 int newdist = dist[u] + c[u][j];
54                 if(newdist < dist[j])
55                 {
56                     dist[j] = newdist;
57                     prev[j] = u;
58                 }
59             }
60     }
61 }
62
63 // 查找从源点v到终点u的路径，并输出
64 void searchPath(int *prev,int v, int u)
65 {
66     int que[maxnum];
67     int tot = 1;
68     que[tot] = u;
69     tot++;
70     int tmp = prev[u];
71     while(tmp != v)
72     {
73         que[tot] = tmp;
74         tot++;
75         tmp = prev[tmp];
76     }
77     que[tot] = v;
78     for(int i=tot; i>=1; --i)
79         if(i != 1)
80             cout << que[i] << " -> ";
81         else
82             cout << que[i] << endl;
83 }
84
85 int main()
86 {
87     freopen("input.txt", "r", stdin);
88     // 各数组都从下标1开始
89
90     // 输入结点数
91     cin >> n;
92     // 输入路径数
93     cin >> line;
94     int p, q, len;          // 输入p, q两点及其路径长度
95
96     // 初始化c[][]为maxint
97     for(int i=1; i<=n; ++i)
98         for(int j=1; j<=n; ++j)
99             c[i][j] = maxint;
100
101     for(int i=1; i<=line; ++i)
102     {
103         cin >> p >> q >> len;
104         if(len < c[p][q])       // 有重边
105         {
106             c[p][q] = len;      // p指向q
107             c[q][p] = len;      // q指向p，这样表示无向图
108         }
109     }
110
111     for(int i=1; i<=n; ++i)
112         dist[i] = maxint;
113     for(int i=1; i<=n; ++i)
114     {
115         for(int j=1; j<=n; ++j)
116             printf("%8d", c[i][j]);
117         printf("\n");
118     }
119
120     Dijkstra(n, 1, dist, prev, c);
121
122     // 最短路径长度
123     cout << "源点到最后一个顶点的最短路径长度: " << dist[n] << endl;
124
125     // 路径
126     cout << "源点到最后一个顶点的路径为: ";
127     searchPath(prev, 1, n);
128 }

输入数据:
5
7
1 2 10
1 4 30
1 5 100
2 3 50
3 5 10
4 3 20
4 5 60
输出数据:
999999 10 999999 30 100
10 999999 50 999999 999999
999999 50 999999 20 10
30 999999 20 999999 60
100 999999 10 60 999999
源点到最后一个顶点的最短路径长度: 60
源点到最后一个顶点的路径为: 1 -> 4 -> 3 -> 5

本文转自：http://www.wutianqi.com/?p=1890
其他连接：http://2728green-rock.blog.163.com/blog/static/43636790200901211848284/

posted @ 2012-06-30 16:12 王海光阅读(528) | 评论 (0) | 编辑收藏

贪心算法

一．贪心算法的基本概念

当一个问题具有最优子结构性质时，我们会想到用动态规划法去解它。但有时会有更简单有效的算法。我们来看一个找硬币的例子。假设有四种硬币，它们的面值分别为二角五分、一角、五分和一分。现在要找给某顾客六角三分钱。这时，我们会不假思索地拿出2个二角五分的硬币，1个一角的硬币和3个一分的硬币交给顾客。这种找硬币方法与其他的找法相比，所拿出的硬币个数是最少的。这里，我们下意识地使用了这样的找硬币算法：首先选出一个面值不超过六角三分的最大硬币，即二角五分；然后从六角三分中减去二角五分，剩下三角八分；再选出一个面值不超过三角八分的最大硬币，即又一个二角五分，如此一直做下去。这个找硬币的方法实际上就是贪心算法。顾名思义，贪心算法总是作出在当前看来是最好的选择。也就是说贪心算法并不从整体最优上加以考虑，它所作出的选择只是在某种意义上的局部最优选择。当然，我们希望贪心算法得到的最终结果也是整体最优的。上面所说的找硬币算法得到的结果就是一个整体最优解。找硬币问题本身具有最优子结构性质，它可以用动态规划算法来解。但我们看到，用贪心算法更简单，更直接且解题效率更高。这利用了问题本身的一些特性。例如，上述找硬币的算法利用了硬币面值的特殊性。如果硬币的面值改为一分、五分和一角一分3种，而要找给顾客的是一角五分钱。还用贪心算法，我们将找给顾客1个一角一分的硬币和4个一分的硬币。然而3个五分的硬币显然是最好的找法。虽然贪心算法不是对所有问题都能得到整体最优解，但对范围相当广的许多问题它能产生整体最优解。如图的单源最短路径问题，最小生成树问题等。在一些情况下，即使贪心算法不能得到整体最优解，但其最终结果却是最优解的很好的近似解。

二．求解活动安排问题算法

活动安排问题是可以用贪心算法有效求解的一个很好的例子。该问题要求高效地安排一系列争用某一公共资源的活动。贪心算法提供了一个简单、漂亮的方法使得尽可能多的活动能兼容地使用公共资源。

设有n个活动的集合e={1，2，…，n}，其中每个活动都要求使用同一资源，如演讲会场等，而在同一时间内只有一个活动能使用这一资源。每个活动i都有一个要求使用该资源的起始时间si和一个结束时间f_i,且s_i<f_i。如果选择了活动i，则它在半开时间区间[s_i，f_i]内占用资源。若区间[s_i，f_i]与区间[s_j，f_j]不相交，则称活动i与活动j是相容的。也就是说，当s_i≥fi或s_j≥f_j时，活动i与活动j相容。活动安排问题就是要在所给的活动集合中选出最大的相容活动子集合。

在下面所给出的解活动安排问题的贪心算法gpeedyselector中，各活动的起始时间和结束时间存储于数组s和f{中且按结束时间的非减序：．f1≤f2≤…≤fn排列。如果所给出的活动未按此序排列，我们可以用o(nlogn)的时间将它重排。

1 template< class type>
2
3 void greedyselector(int n, type s[ 1, type f[ ], bool a[ ] ]
4
5 {
6      a[ 1 ] = true;
7
8      int j = 1;
9
10      for (int i=2;i< =n;i+ + )
11      {
12
13           if (s[i]>=f[j])
14           {
15
16                 a[i] = true;
17
18                 j=i;
19           }
20           else
21                 a[i]= false;
22     }
23 }

算法greedyselector中用集合a来存储所选择的活动。活动i在集合a中，当且仅当a[i]的值为true。变量j用以记录最近一次加入到a中的活动。由于输入的活动是按其结束时间的非减序排列的，f_j总是当前集合a中所有活动的最大结束时间，即：

贪心算法greedyselector一开始选择活动1，并将j初始化为1。然后依次检查活动i是否与当前已选择的所有活动相容。若相容则将活动i加人到已选择活动的集合a中，否则不选择活动i，而继续检查下一活动与集合a中活动的相容性。由于f_i

总是当前集合a中所有活动的最大结束时间，故活动i与当前集合a中所有活动相容的充分且必要的条件是其开始时间s不早于最近加入集合a中的活动j的结束时间f_j，s_i≥f_j。若活动i与之相容，则i成为最近加人集合a中的活动，因而取代活动j的位置。由于输人的活动是以其完成时间的非减序排列的，所以算法greedyselector每次总是选择具有最早完成时间的相容活动加入集合a中。直观上按这种方法选择相容活动就为未安排活动留下尽可能多的时间。也就是说，该算法的贪心选择的意义是使剩余的可安排时间段极大化，以便安排尽可能多的相容活动。算法greedyselector的效率极高。当输人的活动已按结束时间的非减序排列，算法只需g(n)的时间来安排n个活动，使最多的活动能相容地使用公共资源。

例：设待安排的11个活动的开始时间和结束时间按结束时间的非减序排列如下：

i	1	2	3	4	5	6	7	8	9	10	11
s[i]	1	3	0	5	3	5	6	8	8	2	12
f[i]	4	5	6	7	8	9	10	11	12	13	14

算法greedyselector的计算过程如图所示。

图中每行相应于算法的一次迭代。阴影长条表示的活动是已选人集合a中的活动，而空白长条表示的活动是当前正在检查其相容性的活动。

若被检查的活动i的开始时间s_i小于最近选择的活动了的结束时间f_j，则不选择活动i，否则选择活动i加入集合a中。

三．算法分析

贪心算法并不总能求得问题的整体最优解。但对于活动安排问题，贪心算法greedyse—1ector却总能求得的整体最优解，即它最终所确定的相容活动集合a的规模最大。我们可以用数学归纳法来证明这个结论。

事实上，设e={1，2，…，n}为所给的活动集合。由于正中活动按结束时间的非减序排列，故活动1具有最早的完成时间。首先我们要证明活动安排问题有一个最优解以贪心选择开始，即该最优解中包含活动1。设是所给的活动安排问题的一个最优解，且a中活动也按结束时间非减序排列，a中的第一个活动是活动k。若k=1，则a就是一个以贪心选择开始的最优解。若k>1，则我们设。由于f1≤f_k，且a中活动是互为相容的，故b中的活动也是互为相容的。又由于b中活动个数与a中活动个数相同，且a是最优的，故b也是最优的。也就是说b是一个以贪心选择活动1开始的最优活动安排。因此，我们证明了总存在一个以贪心选择开始的最优活动安排方案。

进一步，在作了贪心选择，即选择了活动1后，原问题就简化为对e中所有与活动1相容的活动进行活动安排的子问题。即若a是原问题的一个最优解，则a’=a—{i}是活动安排问题的一个最优解。事实上，如果我们能找到e’的一个解b’，它包含比a’更多的活动，则将活动1加入到b’中将产生e的一个解b，它包含比a更多的活动。这与a的最优性矛盾。因此，每一步所作的贪心选择都将问题简化为一个更小的与原问题具有相同形式的子问题。对贪心选择次数用数学归纳法即知，贪心算法greedyselector最终产生原问题的一个最优解。

四．贪心算法的基本要素

贪心算法通过一系列的选择来得到一个问题的解。它所作的每一个选择都是当前状态下某种意义的最好选择，即贪心选择。希望通过每次所作的贪心选择导致最终结果是问题的一个最优解。这种启发式的策略并不总能奏效，然而在许多情况下确能达到预期的目的。解活动安排问题的贪心算法就是一个例子。下面我们着重讨论可以用贪心算法求解的问题的一般特征。

对于一个具体的问题，我们怎么知道是否可用贪心算法来解此问题，以及能否得到问题的一个最优解呢?这个问题很难给予肯定的回答。但是，从许多可以用贪心算法求解的问题中

我们看到它们一般具有两个重要的性质：贪心选择性质和最优子结构性质。

1．贪心选择性质

所谓贪心选择性质是指所求问题的整体最优解可以通过一系列局部最优的选择，即贪心选择来达到。这是贪心算法可行的第一个基本要素，也是贪心算法与动态规划算法的主要区别。在动态规划算法中，每步所作的选择往往依赖于相关子问题的解。因而只有在解出相关子问题后，才能作出选择。而在贪心算法中，仅在当前状态下作出最好选择，即局部最优选择。然后再去解作出这个选择后产生的相应的子问题。贪心算法所作的贪心选择可以依赖于以往所作过的选择，但决不依赖于将来所作的选择，也不依赖于子问题的解。正是由于这种差别，动态规划算法通常以自底向上的方式解各子问题，而贪心算法则通常以自顶向下的方式进行,以迭代的方式作出相继的贪心选择，每作一次贪心选择就将所求问题简化为一个规模更小的子问题。

对于一个具体问题，要确定它是否具有贪心选择性质，我们必须证明每一步所作的贪心选择最终导致问题的一个整体最优解。通常可以用我们在证明活动安排问题的贪心选择性质时所采用的方法来证明。首先考察问题的一个整体最优解，并证明可修改这个最优解，使其以贪心选择开始。而且作了贪心选择后，原问题简化为一个规模更小的类似子问题。然后，用数学归纳法证明，通过每一步作贪心选择，最终可得到问题的一个整体最优解。其中，证明贪心选择后的问题简化为规模更小的类似子问题的关键在于利用该问题的最优子结构性质。

2．最优子结构性质

当一个问题的最优解包含着它的子问题的最优解时，称此问题具有最优子结构性质。问题所具有的这个性质是该问题可用动态规划算法或贪心算法求解的一个关键特征。在活动安排问题中，其最优子结构性质表现为：若a是对于正的活动安排问题包含活动1的一个最优解,则相容活动集合a’=a—{1}是对于e’={i∈e:s_i≥f₁}的活动安排问题的一个最优解。

3．贪心算法与动态规划算法的差异

贪心算法和动态规划算法都要求问题具有最优子结构性质，这是两类算法的一个共同点。但是，对于一个具有最优子结构的问题应该选用贪心算法还是动态规划算法来求解?是不是能用动态规划算法求解的问题也能用贪心算法来求解?下面我们来研究两个经典的组合优化问题，并以此来说明贪心算法与动态规划算法的主要差别。

五． ０－背包问题

给定n种物品和一个背包。物品i的重量是w，其价值为v，背包的容量为c.问应如何选择装入背包中的物品，使得装入背包中物品的总价值最大? 在选择装入背包的物品时，对每种物品i只有两种选择，即装入背包或不装入背包。不能将物品i装入背包多次，也不能只装入部分的物品i。

此问题的形式化描述是，给定c>0，w_i>0，v_i>0，1≤i≤n，要求找出一个n元0—1向

量(xl，x2，…，x_n)，，使得≤c，而且达到最大。

背包问题：与0-1背包问题类似，所不同的是在选择物品i装入背包时，可以选择物品i的一部分，而不一定要全部装入背包。

此问题的形式化描述是，给定c>0，w_i>0，v_i>0，1≤i≤n，要求找出一个n元向量

(x1,x2,...x_n)，0≤x_i≤1，1≤i≤n 使得≤c，而且达到最大。

这两类问题都具有最优子结构性质。对于0—1背包问题，设a是能够装入容量为c的背包的具有最大价值的物品集合，则a_j=a-{j}是n-1个物品1，2，…，j—1，j+1，…，n可装入容量为c-w_i叫的背包的具有最大价值的物品集合。对于背包问题，类似地，若它的一个最优解包含物品j，则从该最优解中拿出所含的物品j的那部分重量w_i，剩余的将是n-1个原重物品1，2，…，j-1，j+1，…，n以及重为w_j-w_i的物品j中可装入容量为c-w的背包且具有最大价值的物品。

虽然这两个问题极为相似，但背包问题可以用贪心算法求解，而0·1背包问题却不能用贪心算法求解。用贪心算法解背包问题的基本步骤是，首先计算每种物品单位重量的价值

v_j／w_i然后，依贪心选择策略，将尽可能多的单位重量价值最高的物品装入背包。若将这种物品全部装入背包后，背包内的物品总重量未超过c，则选择单位重量价值次高的物品并尽可能多地装入背包。依此策略一直进行下去直到背包装满为止。具体算法可描述如下：

void knapsack(int n, float m, float v[ ], float w[ ], float x[ ] )

sort(n,v,w);

int i;

for(i= 1;i<= n;i++) x[i] = o;

float c = m;

for (i = 1;i < = n;i ++) {

if (w[i] > c) break;

x[i] = 1;

c-= w[i];

}

if (i < = n) x[i] = c/w[i];

}

算法knapsack的主要计算时间在于将各种物品依其单位重量的价值从大到小排序。因此，算法的计算时间上界为o(nlogn)。当然，为了证明算法的正确性，我们还必须证明背包问题具有贪心选择性质。

这种贪心选择策略对0—1背包问题就不适用了。看图2(a)中的例子，背包的容量为50千克；物品1重10千克；价值60元；物品2重20千克，价值100元；物品3重30千克；价值120元。因此，物品1每千克价值6元，物品2每千克价值5元，物品3每千克价值4元。若依贪心选择策略，应首选物品1装入背包，然而从图4—2(b)的各种情况可以看出，最优的选择方案是选择物品2和物品3装入背包。首选物品1的两种方案都不是最优的。对于背包问题，贪心选择最终可得到最优解，其选择方案如图2(c)所示。

对于0—1背包问题，贪心选择之所以不能得到最优解是因为它无法保证最终能将背包装满，部分背包空间的闲置使每千克背包空间所具有的价值降低了。事实上，在考虑0—1背包问题的物品选择时，应比较选择该物品和不选择该物品所导致的最终结果，然后再作出最好选择。由此就导出许多互相重叠的于问题。这正是该问题可用动态规划算法求解的另一重要特征。动态规划算法的确可以有效地解0—1背包问题。

本文转自：http://www.cppblog.com/3522021224/archive/2007/06/16/26429.aspx
其他链接：http://www.cnblogs.com/chinazhangjie/archive/2010/11/23/1885330.html

posted @ 2012-06-30 15:55 王海光阅读(374) | 评论 (0) | 编辑收藏

sqlite3 分页

Select * From user Limit 3 Offset 5;

以上语句表示从Account表获取数据，跳过5行，取3行

用法一

SELECT `keyword_rank`.* FROM `keyword_rank` WHERE (advertiserid='59') LIMIT 2 OFFSET 1;

比如这个SQL ，limit后面跟的是2条数据，offset后面是从第1条开始读取。

用法二

SELECT `keyword_rank`.* FROM `keyword_rank` WHERE (advertiserid='59') LIMIT 2,1;

而这个SQL，limit后面是从第2条开始读，读取1条信息。

这两个千万别搞混哦。

用法三

select * from tablename <条件语句> limit 100,-1

从第100条后开始-最后一条的记录

用法四

select * from tablename <条件语句> limit 15

相当于limit 0,15 .查询结果取前15条数据

用法五
mysql低版本不支持limit offset
limit offset 在mysql 4.0以上的版本中都可以正常运行，在旧版本的mysql 3.23中无效
limit m offset n 等价于 limit m,n

limit 的优化

mysql的limit给分页带来了极大的方便，但数据量一大的时候，limit的性能就急剧下降

来源：一亩三分地博客
MYSQL的优化是非常重要的。其他最常用也最需要优化的就是limit。mysql的limit给分页带来了极大的方便，但数据量一大的时候，limit的性能就急剧下降。

同样是取10条数据

select * from yanxue8_visit limit 10000,10 和
select * from yanxue8_visit limit 0,10
就不是一个数量级别的。

网上也很多关于limit的五条优化准则，都是翻译自mysql手册，虽然正确但不实用。今天发现一篇文章写了些关于limit优化的，很不错。

文中不是直接使用limit，而是首先获取到offset的id然后直接使用limit size来获取数据。根据他的数据，明显要好于直接使用limit。这里我具体使用数据分两种情况进行测试。（测试环境win2033+p4双核 (3GHZ) +4G内存 mysql 5.0.19）

1、offset比较小的时候。

select * from yanxue8_visit limit 10,10

多次运行，时间保持在0.0004-0.0005之间
Select * From yanxue8_visit Where vid ＞=(
Select vid From yanxue8_visit Order By vid limit 10,1
) limit 10

多次运行，时间保持在0.0005-0.0006之间，主要是0.0006
结论：偏移offset较小的时候，直接使用limit较优。这个显然是子查询的原因。

2、offset大的时候。
select * from yanxue8_visit limit 10000,10

多次运行，时间保持在0.0187左右
Select * From yanxue8_visit Where vid ＞=(
Select vid From yanxue8_visit Order By vid limit 10000,1
) limit 10

多次运行，时间保持在0.0061左右，只有前者的1/3。可以预计offset越大，后者越优
本文转自：http://blog.csdn.net/lvwz2008/article/details/7558285

posted @ 2012-06-21 12:40 王海光阅读(1221) | 评论 (0) | 编辑收藏

BAT命令

摘要: 1.批处理文件是一个“.bat”结尾的文本文件，这个文件的每一行都是一条DOS命令。可以使用任何文本文件编辑工具创建和修改。 2.批处理是一种简单的程序，可以用 if 和 goto 来控制流程，也可以使用 for 循环。 3.批处理的编程能力远不如C语言等编程语言，也十分不规范。 4.每个编写好的批处理文件都相当于一个DOS的外部命令，把它所在的目录放到DOS搜索路径(path)中，即可在任意位置运行。 5.C:\AUTOEXEC.BAT 是每次系统启动时都会自动运行的，可以将每次启动时都要运行的命令放入该文件中。 6.大小写不敏感(命令符忽略大小写) 7.批处理的文件扩展名为 .bat 或 .cmd。阅读全文

posted @ 2012-06-21 12:30 王海光阅读(3148) | 评论 (0) | 编辑收藏

VC 按钮添加图标,位图

【按钮添加图标】

方法一:

1.添加图标资源IDI_ICON1;

2 使用函数 LoadIcon() 载入图标。因为LoadIcon() 是类 CWinApp 的成员函数，同时函数 LoadIcon() 返回所载入图标的句柄。所以我们采用以下方法来调用函数 LoadIcon():

HICON m_hicn1=AfxGetApp()->LoadIcon(IDI_ICON1);

3 为按钮设置图标了，这通过调用函数 SetIcon() 来实现:

m_button1.SetIcon(m_hicn1); // m_button1是按钮变量

方法二:

前两步和上方法一样;

3 先由函数 GetDlgItem() 获得一个指向 CWnd 对象的指针，再通过强制类型转换将该指针转换为一个指向 CButton 类对象的指针。进而通过该指针来调用函数 SetIcon()。具体实现代码如下：

CWnd *pWnd = GetDlgItem(IDC_BUTTON1);
CButton *Button= (CButton *) pWnd;
Button-> SetIcon(m_hicn1);

【按钮添加位图】

1 添加位图资源BMP1;

2 利用函数 LoadBitmap() 从资源中载入位图.

HBITMAP LoadBitmap(
HINSTANCE hInstance, // handle of application instance
LPCTSTR lpBitmapName // address of bitmap resource name
);

所以，为达到载入位图的目的，不仅要定义一个位图句柄 hBitmap，而且还要定义一个应用程序实例句柄 hInstance，

并调用函数 AfxGetInstanceHandle() 以获得当前的应用程序实例句柄，代码如下：

HBITMAP hBitmap;

HINSTANCE hInstance = ::AfxGetInstanceHandle();

只有在声明并获得了当前的应用程序句柄后，才能使用以下语句载入位图：

hBitmap = ::LoadBitmap(hInstance,"BMP1"); //BMP1是资源文件名

3 用SetBitmap()添加位图;

m_button1.SetBitmap(hBitmap);

或

pWnd = GetDlgItem(IDC_BUTTON1);
Button= (CButton *) pWnd;
Button-> SetBitmap(hBitmap);

___________________________________________________

位图按钮的实现方法：
首先，我们创建一个基于对话框的应用程序CmyDialog    ；
Ι．MFC的CBitmapButton类，这也是最简单的功能最强的位图按钮。我们可以采取如下的步骤：
1．为按钮指定唯一的按钮标题（此例子为OK按钮，这里设置按钮标题为OK）并选中Ownerdraw属性，然后在项目中加一些位图资源，并用名字标示这些资源而不要用数字ID，其ID分别为”OKU”、”OKD”、”OKF”、”OKX”（一定要加双引号），分别对应于按钮的“松开(Up)”、“按下(Down)”、“获得输入焦点(focused)”和“禁止(Disable)”状态。
2．我们还要在对话框类中加入CBitmapButton    m_aBmpBtn;数据成员。
3．在初始化中为这个成员调用：
…
m_aBmpBtn.    AutoLoad(IDOK,this);
…
点击编译按钮，成功后运行程序，我们的位图按钮已经建立了。
改变CANCLE按钮的标题，可以设置其标题为ICON或者BITMAP    ：（这里我们演示了bitmap的用法，Icon按钮读者可以按照下面的代码处理）

CBitmapButton的使用
CBitmapButton作为MFC的控件类，并不为很多人所使用，因为现在网上遍布着从CButton派生的各种各样的按钮类，其中最为著名的就是CButtonST类了。但是最近在CSDN上看到几个问题都是使用CBitmapButton类，但是由于使用错误、不当而造成程序崩溃或者错误的。所以总结一下CBitmapButton类的使用，希望能帮助一些初学者。
可以参考MSDN自带的例子“CTRLTEST”学习CBitmapButton的用法。个人总结如下：
1、在资源编辑的时候选中按钮的Owner draw即可，不需要选择Bitmap属性！
2、在程序中定义一个CBitmapButton成员变量。不能使用ClassWizard为按钮映射一个CButton变量，然后改为CBitmapButton，这么做并不能将按钮直接映射为CBitmapButton类的对象，反而会出现初始化错误。也不能两种变量同时存在,会造成程序崩溃。
3-1、使用CBitmapButton::LoadBitmaps装载各种状态的图片,使用SubclassDlgItem关联到想要的按钮，使用CBitmapButton::SizeToContent函数使按钮适合图片大小。。注意Loadbitmaps一定要在关联到按钮之前进行！
3-2、或者是使用CBitmapButton::AutoLoad函数关联到想要的按钮。需要注意：
A、之前不能使用CBitmapButton::LoadBitmaps装载各种状态的图片，否则会出错。
B、AutoLoad函数完成的关联和改变按钮大小的CBitmapButton::SizeToContent函数的功能。
C、CBitmapButton::AutoLoad使用的位图是默认资源ID的，即它会自动装载相关资源位图。位图的资源ID格式为："按钮Caption+U"、"按钮Caption+D"、"按钮Caption+F"、"按钮Caption+X"，分别代表Up、Down、Focus、Disable状态。如资源编辑时，希望关联的按钮的Caption为Test，那么其默认装载的位图资源的ID为："TestU"/"TestD"/"TestF"/"TestX"，注意分号""也是其ID的一部分。

Ⅱ．使用图标制作按钮
1．打开ICON按钮的属性页，在Style中选中Icon
2．在对话框类的头文件中定义成员变量（使用ClassWizard加入这个成员变量）
CButton    m_IconBtn；//对应于图标按钮
3．创建相应的图标或者位图资源：
图标资源：IDI_ICONBUTTON
4．在初始化中加入如下代码：
…
//对应于图标按钮
HICON hIcon=AfxGetApp()->LoadIcon(IDI_ICONBUTTON);
m_IconBtn.SetIcon(hIcon);
…
重新编译运行我们的程序，奇妙的图像按钮呈现在我们的眼前了。

Ⅲ．使用位图制作按钮
1．打开BITMAP按钮的属性页，在Style中选中Bitmap。
2．对话框类的头文件中定义成员变量（使用ClassWizard加入这个成员变量）
CButton    m_IconBtn；
3．创建位图资源：
位图资源：IDB_BITMAPBUTTON
4．在初始化中加入如下代码：
//对应于位图按钮
…
HBITMAP    hBmp=::LoadBitmap(AfxGetInstanceHandle(),
MAKEINTRESOURCE(IDB_    BITMAPBUTTON));
m_BmpBtn.SetBitmap(hBmp);

本文转自：http://hi.baidu.com/lechie/item/dcbca9f4ee98a3d742c36ad4

posted @ 2012-06-18 17:32 王海光阅读(1691) | 评论 (0) | 编辑收藏

COM入门

摘要: 本文转自：http://www.vckbase.com/document/viewdoc/?id=212 本文的目的是为刚刚接触COM的程序员提供编程指南，并帮助他们理解COM的基本概念。内容包括COM规范简介，重要的COM术语以及如何重用现有的COM组件。本文不包括如何编写自己的COM对象和接口。　　COM即组件对象模型，是Compone... 阅读全文

posted @ 2012-06-11 14:58 王海光阅读(708) | 评论 (0) | 编辑收藏

ATL入门：利用ATL编写简单的COM组件（转）

使用ATL编写一个简单的COM服务器
      本文的对象是COM编程初学者，其目的旨在描述如何用ATL创建COM服务器，以及如何在VC或VB编写的客户端应用程序中调用COM服务器。为了不给初学者增加负担，本文不打算深入讨论COM和IDL的细节，而是展示用ATL创建简单的COM对象所需要的步骤。希望通过这篇文章能刺激你学习COM编程的欲望。

第一步：运行ATL COM向导
    你要做的第一件事情是启动VS2008创建一个新的工程。选择“File->New Project”。弹出创建工程对话框，选择"Visual C++->ATL->ATL Project"，在下面输入工程名称和路径,注意这个向导创建的工程并没有包含任何初始的COM对象，在完成这个向导之后，要从“ClassView”中用“New ATL Object”命令来指定你想要增加到这个工程中的对象类型。然后单击"OK"按钮。
    第一部分单选按钮选项是要创建的服务器类型“Server Type”。因为我们要创建一个进程内服务器（Server DLL），所以应该选择的类型是动态链接库“Dynamic Link Library——DLL”，注意所有进程内服务器都是DLL。下面是三个复选框不用去管它，它和我们创建的这个工程没关系。单击“Finish”按钮。

第二步：创建新的ATL对象
     为你的ATL项目（容器）添加供外部使用的Class (ATL Simple Object)。选项页 “ C++”的“Short name”输入栏中输入你的Class名称，其它输入框会自动更新。
    “Threading model”选“Apartment”;“Interface”选“Dual”;“Aggregation”选“No”;“Support”选“Connection points”和“I Object With Site(IE objects support)”。
     在“Short Name”文本编辑框中输入“First_ATL”。注意向导会自动填写其余的文本编辑框。单击“Attributes”标签。其中有几组单选按钮选项和几个复选框。第一组单选按钮是线程模型“Threading Model”，我们取缺省值“Apartment Model”。第二组单选按钮是接口“Interface”，单击“Dual”，也就是双接口。最后，第三组单选按钮是聚合“Aggregation”，因为我们不想涉及接口的聚合，所以在此选择“No”。至于底下的三个复选框，我们不用管它，单击OK按钮让向导创建新的“ATL Simple Object”

第三步：添加方法
   如果你单击工作间的“ClassView”标签，你会注意到向导在里面添加了一些内容。添加一个方法很容易，选中“IFirst_ATL”后单击右键并选择“Add Method”。
   单击“Add Method”后，你会看到“Add Method to Interface”对话框。
    在“Return Type”编辑框中（已成灰色）这个方法的返回值已经缺省为 “HRESULT”。大多数情况下都应该是这个值类型。下一个编辑框是方法名“Method Name”，输入方法名“AddNumbers”。最后一个编辑框是要你输入希望使用的参数“Parameters”。由于我们打算将两个数字相加，然后返回相加结果，所以要使用三个参数。最后一个参数是一个指针。现在你不用去关心繁杂的接口定义语言IDL，只要在这个参数编辑框中输入如下内容：
[in] long Num1, [in] long Num2, [out] long *ReturnVal
它的意思是声明两个long类型输入[in]参数和一个指针返回值[out]（刚开始可能会不习惯这样怪怪的写法，但等你阅读了一两本关于COM的书之后，会慢慢接收它的）。单击OK按钮。展开所有“ClassView”的节点“+”号。从这个视图可以清楚地了解Simple_ATL各个类之间的层次关系。双击最上面“IFirst_ATL”（接口）节点下的“AddNumbers”（方法）节点，右边屏幕将会显示这个方法的实现代码。添加如下的代码：

1 STDMETHODIMP CFirst_ATL::AddNumbers(long Num1, long Num2, long *ReturnVal)
2 {
3 // TODO: Add your implementation code here
4 *ReturnVal = Num1 + Num2;
5
6 return S_OK;
7 }

第四步：编译这个DLL
不管你想不相信，到目前为止，我们用ATL所创建的COM服务器已经完全能运行！当然，还需要编译它才行。按下“F7”功能键，几秒钟之后，VC++便会完成编译并注册你所创建的DLL服务器。这样其它的应用程序就可以使用这个COM服务器了。试一试吧！

第五步：用VC测试这个服务器
保存并关闭Simple_ATL工程，然后创建一个新的Win32 控制台应用程序。选择“Win32 Console Application”并取名为“Test_ATL”。单击OK按钮并接受对话框中的缺省设置（空的工程）。单击“Finish”按钮，然后再按OK按钮。这样就创建好了一个空的工程。按下“Control+N”键向工程中添加一个文件。从弹出的窗口中选择“C++ Source File”并为它取名为“Test_ATL.cpp”。按下OK按钮。这样工程中就有了一个空的.CPP文件。我们要在这个文件中添加一些测试COM服务器的代码：
// 将头文件的目录指到Simple_ATL工程所在的目录

1 #include "stdafx.h"
2 #include "..\..\Simple_ATL\Simple_ATL\Simple_ATL_i.h"
3 #include "..\..\Simple_ATL\Simple_ATL\Simple_ATL_i.c"
4 #include <iostream>
5 using namespace std;
6 // 从Simple_ATL 工程所在目录的Simple_ATL_i.c 文件中拷贝以下内容
7 // 注意: 你也可以不拷贝这些东西，而是把文件Simple_ATL_i.c包含进来。
8 // 我之所以将它拷进来，是想更清楚地展示这些敞亮来自什么地方一击它们的代码
9 // const IID IID_IFirst_ATL =
10 // {0x5AC2B2B7,0xBA06,0x4A4E,0x8D,0xED,0x78,0xDD,0x95,0x73,0x25,0x3B};
11 //
12 // const CLSID CLSID_First_ATL =
13 // {0x862DFA11,0x863B,0x4115,0xB7,0x39,0xB6,0x18,0x0E,0xBC,0x6B,0x66};
14
15 void main(void)
16 {
17     // 声明HRESULT和Simple_ATL接口指针
18     HRESULT  hr;
19     IFirst_ATL *IFirstATL = NULL;
20
21     // 初始化COM
22     hr = CoInitialize(0);
23
24     // 使用SUCCEEDED 宏并检查我们是否能得到一个接口指针
25     if(SUCCEEDED(hr))
26     {
27         hr = CoCreateInstance( CLSID_First_ATL, NULL, CLSCTX_INPROC_SERVER,
28             IID_IFirst_ATL, (void**) &IFirstATL);
29
30         // 如果成功，则调用AddNumbers方法，否则显示相应的出错信息
31         if(SUCCEEDED(hr))
32         {
33             long ReturnValue;
34
35             IFirstATL->AddNumbers(5, 7, &ReturnValue);
36             cout << "The answer for 5 + 7 is: " << ReturnValue << endl;
37             IFirstATL->Release();
38         }
39         else
40         {
41             cout << "CoCreateInstance Failed." << endl;
42         }
43     }
44     // 释放COM
45     CoUninitialize();
46 }

第七步：编译并运行测试程序
按下“F5”功能键，编译测试程序，然后按“Control+F5”功能组合键运行测试程序。在DOS窗口中，你应该能看到输出的结果。

本文转自：http://andylin02.iteye.com/blog/453079。

posted @ 2012-06-07 13:56 王海光阅读(1453) | 评论 (0) | 编辑收藏

Linux下C++程序常用编译命令

本文转自：http://blog.csdn.net/lee353086/article/details/5864939

Linux下C++程序常用编译命令

文中涉及的命令在Ubuntu8.04.1中测试通过，本文的目的是为了以后要用的时候，只要看一下本文就马上能回忆起这此命令怎么用。

生成目标文件

#gcc –c <XXX.cpp>

可以有多个cpp文件

编译静态库

#ar cr <libXXX.a> <XXX.o>

可以有多个o文件（目标文件）

静态库名的命名方式应该是libXXX.a 其中XXX是库的名字。

编译成动态库

# gcc -shared -fPCI -o libmyhello.so hello.o

可以有多个o文件，若考虑到同个库有多个版本，参考如下命令

#gcc -shared -Wl,-soname,libhello.so.1 -o libhello.so.1.0 hello.o

另外再建立两个符号连接：

#ln -s libhello.so.1.0 libhello.so.1

#ln -s libhello.so.1 libhello.so 这样一个libhello的动态连接库就生成了。最重要的是传gcc -shared 参数使其生成是动态库而不是普通执行程序。

-Wl 表示后面的参数也就是-soname,libhello.so.1直接传给连接器ld进行处理。实际上，每一个库都有一个soname，当连接器发现它正在查找的程序库中有这样一个名称，连接器便会将soname嵌入连结中的二进制文件内，而不是它正在运行的实际文件名，在程序执行期间，程序会查找拥有 soname名字的文件，而不是库的文件名，换句话说，soname是库的区分标志。这样做的目的主要是允许系统中多个版本的库文件共存，习惯上在命名库文件的时候通常与soname相同 libxxxx.so.major.minor 其中，xxxx是库的名字，major是主版本号，minor 是次版本号

使用静态库

#gcc –o <输出文件名> <目标文件名> <静态库文件名>

使用动态库

#gcc <源文件名> -l<动态库文件名> -L<动态库所在路径>

例如：

#gcc test.c -lhello -L.

把源test.c编译为a.out可执行文件，test.c所需要的函数在libhello.so文件中定义，libhello.so文件在当前目录。

直接执行a.out提示找不到动态库文件，这时需要修改当前的动态库搜索路径。

如下：

# export LD_LIBRARY_PATH=.:$LD_LIBRARY_PATH

再执行a.out，测试文件运行成功。

常用命令

[1]查看当前文件依赖于哪些库

#ldd <库文件或可执行文件>

[2]查看文件类型

#file <可执行文件名>

[3]查看库中符号

#nm <库文件名称>

nm列出的符号有很多，常见的有三种，一种是在库中被调用，但并没有在库中定义(表明需要其他库支持)，用U表示；一种是库中定义的函数，用T表示，这是最常见的；另外一种是所谓的“弱态”符号，它们虽然在库中被定义，但是可能被其他库中的同名符号覆盖，用W表示。

通常和grep命令配合使用

可执行程序在执行的时候如何定位共享库文件

采用以下顺序

[搜索elf文件的 DT_RPATH段]=>

[ 环境变量LD_LIBRARY_PATH]=>

[/etc/ld.so.cache文件列表]=>

[/lib/,/usr/lib目录]

如何让执行程序顺利找到动态库

[方法一]把库文件copy到/usr/lib目录或/lib目录。

[方法二]修改当前终端的LD_LIBRARY_PATH环境变量，例如：

#export LD_LIBRARY_PATH=$LD_LIBRARY_PATH:/home/WhereIsMyLibLocation

此方法只能临时改变搜索路径

[方法三]修改/etc/ld.so.conf文件，把库所在的路径加到文件末尾，并执行ldconfig刷新。这样，加入的目录下的所有库文件都可见。

常用参数（速记）

-I<头文件路径> -L<库文件路径> -i<头文件> -l<库文件名>

-Wall 尽可能多的警告信息

-o 输出可执行文件名（起到重命名输出文件名的作用）

比如说用gcc编译C++文件需要加上-lstdc++参数，让编译器去找libstdc++.a静态库文件

posted @ 2012-06-07 10:55 王海光阅读(549) | 评论 (0) | 编辑收藏

STL迭代器及总结

解释
      迭代器是一种对象，它能够用来遍历STL容器中的部分或全部元素，每个迭代器对象代表容器中的确定的地址。迭代器修改了常规指针的接口，所谓迭代器是一种概念上的抽象：那些行为上象迭代器的东西都可以叫做迭代器。然而迭代器有很多不同的能力，它可以把抽象容器和通用算法有机的统一起来。
      迭代器提供一些基本操作符：*、++、==、！=、=。这些操作和C/C++“操作array元素”时的指针接口一致。不同之处在于，迭代器是个所谓的smart pointers，具有遍历复杂数据结构的能力。其下层运行机制取决于其所遍历的数据结构。因此，每一种容器型别都必须提供自己的迭代器。事实上每一种容器都将其迭代器以嵌套的方式定义于内部。因此各种迭代器的接口相同，型别却不同。这直接导出了泛型程序设计的概念：所有操作行为都使用相同接口，虽然它们的型别不同。

功能特点
      迭代器使开发人员不必整个实现类接口。只需提供一个迭代器，即可遍历类中的数据结构，可被用来访问一个容器类的所包函的全部元素，其行为像一个指针，但是只可被进行增加(++)或减少(--)操作。举一个例子，你可用一个迭代器来实现对vector容器中所含元素的遍历。
      如下代码对vector容器对象生成和使用了迭代器：

1 vector<int> the_vector;
2 vector<int>::iterator the_iterator;
3     for( int i=0; i < 10; i++ )
4 the_vector.push_back(i);
5 int total = 0;
6 the_iterator = the_vector.begin();
7 while( the_iterator != the_vector.end() )
8 {
9     total += *the_iterator;
10     the_iterator++;
11 }
12 cout << "Total=" << total << endl;

提示：通过对一个迭代器的解引用操作（*），可以访问到容器所包含的元素。

C++标准库总结

容器
序列
      vector=========================<vector>
      list===========================<list>
      deque==========================<deque>

序列适配器
      stack:top,push,pop=============<stack>
      queue:front,back,push,pop======<queue>
      priority_queue:top,push,pop====<queue>

关联容器
      map============================<map>
      multimap=======================<map>
      set============================<set>
      multiset=======================<set>

拟容器
      string=========================<string>
      valarray=======================<valarray>
      bitset=========================<bitset>

算法
http://www.cplusplus.com/reference/algorithm/      STL Algorithms 详细说明。

非修改性序列操作
<algorithm>
      for_each()=====================对序列中每个元素执行操作
      find()=========================在序列中找某个值的第一个出现
      find_if()======================在序列中找符合某谓词的第一个元素
      find_first_of()================在序列中找另一序列里的值
      adjust_find()==================找出相邻的一对值
      count()========================在序列中统计某个值出现的次数
      count_if()=====================在序列中统计与某谓词匹配的次数
      mismatch()=====================找使两序列相异的第一个元素
      equal()========================如果两个序列对应元素都相同则为真
      search()=======================找出一序列作为子序列的第一个出现位置
      find_end()=====================找出一序列作为子序列的最后一个出现位置
      search_n()=====================找出一序列作为子序列的第n个出现位置
修改性的序列操作
<algorithm>
      transform()====================将操作应用于序列中的每个元素
      copy()=========================从序列的第一个元素起进行复制
      copy_backward()================从序列的最后元素起进行复制
      swap()=========================交换两个元素
      iter_swap()====================交换由迭代器所指的两个元素
      swap_ranges()==================交换两个序列中的元素
      replace()======================用一个给定值替换一些元素
      replace_if()===================替换满足谓词的一些元素
      replace_copy()=================复制序列时用一个给定值替换元素
      replace_copy_if()==============复制序列时替换满足谓词的元素
      fill()=========================用一个给定值取代所有元素
      fill_n()=======================用一个给定值取代前n个元素
      generate()=====================用一个操作的结果取代所有元素
      generate_n()===================用一个操作的结果取代前n个元素
      remove()=======================删除具有给定值的元素
      remove_if()====================删除满足谓词的元素
      remove_copy()==================复制序列时删除给定值的元素
      remove_copy_if()===============复制序列时删除满足谓词的元素
      unique()=======================删除相邻的重复元素
      unique_copy()==================复制序列时删除相邻的重复元素
      reexample()======================反转元素的次序
      reexample_copy()=================复制序列时反转元素的次序
      rotate()=======================循环移动元素
      rotate_copy()==================复制序列时循环移动元素
      random_shuffle()===============采用均匀分布随机移动元素
序列排序
<algorithm>
      sort()=========================以很好的平均次序排序
      stable_sort()==================排序且维持相同元素原有的顺序
      partial_sort()=================将序列的前一部分排好序
      partial_sort_copy()============复制的同时将序列的前一部分排好序
      nth_element()==================将第n个元素放到它的正确位置
      lower_bound()==================找到某个值的第一个出现
      upper_bound()==================找到大于某个值的第一个出现
      equal_range()==================找出具有给定值的一个子序列
      binary_search()================在排好序的序列中确定给定元素是否存在
      merge()========================归并两个排好序的序列
      inplace_merge()================归并两个接续的排好序的序列
      partition()====================将满足某谓词的元素都放到前面
      stable_partition()=============将满足某谓词的元素都放到前面且维持原顺序
集合算法
<algorithm>
      include()======================如果一个序列是另一个的子序列则为真
      set_union()====================构造一个已排序的并集
      set_intersection()=============构造一个已排序的交集
      set_difference()===============构造一个已排序序列，包含在第一个序列但不在第二个序列的元素
      set_symmetric_difference()=====构造一个已排序序列，包括所有只在两个序列之一中的元素
堆操作
<algorithm>
      make_heap()====================将序列高速得能够作为堆使用
      push_heap()====================向堆中加入一个元素
      pop_heap()=====================从堆中去除元素
      sort_heap()====================对堆排序
最大和最小
<algorithm>
      min()==========================两个值中较小的
      max()==========================两个值中较大的
      min_element()==================序列中的最小元素
      max_element()==================序列中的最大元素
      lexicographic_compare()========两个序列中按字典序的第一个在前
排列
<algorithm>
      next_permutation()=============按字典序的下一个排列
      prev_permutation()=============按字典序的前一个排列
通用数值算法
<numeric>
      accumulate()===================积累在一个序列中运算的结果(向量的元素求各的推广)
      inner_product()================积累在两个序列中运算的结果(内积)
      partial_sum()==================通过在序列上的运算产生序列(增量变化)
      adjacent_difference()==========通过在序列上的运算产生序列(与partial_sum相反)
C风格算法
<cstdlib>
      qsort()========================快速排序，元素不能有用户定义的构造，拷贝赋值和析构函数
      bsearch()======================二分法查找，元素不能有用户定义的构造，拷贝赋值和析构函数

函数对象
基类
      template<class Arg, class Res> struct unary_function
      template<class Arg, class Arg2, class Res> struct binary_function
谓词
返回bool的函数对象。
<functional>
      equal_to=======================二元，arg1 == arg2
      not_equal_to===================二元，arg1 != arg2
      greater========================二元，arg1 > arg2
      less===========================二元，arg1 < arg2
      greater_equal==================二元，arg1 >= arg2
      less_equal=====================二元，arg1 <= arg2
      logical_and====================二元，arg1 && arg2
      logical_or=====================二元，arg1 || arg2
      logical_not====================一元，!arg
算术函数对象
<functional>
      plus===========================二元，arg1 + arg2
      minus==========================二元，arg1 - arg2
      multiplies=====================二元，arg1 * arg2
      divides========================二元，arg1 / arg2
      modulus========================二元，arg1 % arg2
      negate=========================一元，-arg
约束器，适配器和否定器
<functional>
      bind2nd(y)
            binder2nd==================以y作为第二个参数调用二元函数
      bind1st(x)
            binder1st==================以x作为第一个参数调用二元函数
      mem_fun()
            mem_fun_t==================通过指针调用0元成员函数
            mem_fun1_t=================通过指针调用一元成员函数
            const_mem_fun_t============通过指针调用0元const成员函数
            const_mem_fun1_t===========通过指针调用一元const成员函数
      mem_fun_ref()
            mem_fun_ref_t==============通过引用调用0元成员函数
            mem_fun1_ref_t=============通过引用调用一元成员函数
            const_mem_fun_ref_t========通过引用调用0元const成员函数
            const_mem_fun1_ref_t=======通过引用调用一元const成员函数
      ptr_fun()
            pointer_to_unary_function==调用一元函数指针
      ptr_fun()
            pointer_to_binary_function=调用二元函数指针
      not1()
            unary_negate===============否定一元谓词
      not2()
            binary_negate==============否定二元谓词

迭代器
分类
      Output: *p= , ++
      Input: =*p , -> , ++ , == , !=
      Forward: *p= , =*p , -> , ++ , == , !=
      Bidirectional: *p= , =*p -> , [] , ++ , -- , == , !=
      Random: += , -= , *p= , =*p -> , [] , ++ , -- , + , - , == , != , < , > , <= , >=
插入器
      template<class Cont> back_insert_iterator<Cont> back_inserter(Cont& c);
      template<class Cont> front_insert_iterator<Cont> front_inserter(Cont& c);
      template<class Cont, class Out> insert_iterator<Cont> back_inserter(Cont& c, Out p);
反向迭代器
      reexample_iterator===============rbegin(), rend()
流迭代器
      ostream_iterator===============用于向ostream写入
      istream_iterator===============用于向istream读出
      ostreambuf_iterator============用于向流缓冲区写入
      istreambuf_iterator============用于向流缓冲区读出

分配器
<memory>
      template<class T> class std::allocator

数值
数值的限制
<limits>
      numeric_limits<>
<climits>
      CHAR_BIT
      INT_MAX
      ...
<cfloat>
      DBL_MIN_EXP
      FLT_RADIX
      LDBL_MAX
      ...
标准数学函数
<cmath>
      double abs(double)=============绝对值(不在C中)，同fabs()
      double fabs(double)============绝对值
      double ceil(double d)==========不小于d的最小整数
      double floor(double d)=========不大于d的最大整数
      double sqrt(double d)==========d在平方根，d必须非负
      double pow(double d, double e)=d的e次幂
      double pow(double d, int i)====d的i次幂
      double cos(double)=============余弦
      double sin(double)=============正弦
      double tan(double)=============正切
      double acos(double)============反余弦
      double asin(double)============反正弦
      double atan(double)============反正切
      double atan2(double x,double y) //atan(x/y)
      double sinh(double)============双曲正弦
      double cosh(double)============双曲余弦
      double tanh(double)============双曲正切
      double exp(double)=============指数，以e为底
      double log(double d)===========自动对数(以e为底),d必须大于0
      double log10(double d)=========10底对数，d必须大于0
      double modf(double d,double*p)=返回d的小数部分，整数部分存入*p
      double frexp(double d, int* p)=找出[0.5,1)中的x,y,使d=x*pow(2,y),返回x并将y存入*p
      double fmod(double d,double m)=浮点数余数，符号与d相同
      double ldexp(double d, int i)==d*pow(2,i)
<cstdlib>
      int abs(int)===================绝对值
      long abs(long)=================绝对值(不在C中)
      long labs(long)================绝对值
      struct div_t { implementation_defined quot, rem; }
      struct ldiv_t { implementation_defined quot, rem; }
      div_t div(int n, int d)========用d除n，返回(商，余数)
      ldiv_t div(long n, long d)=====用d除n，返回(商，余数)(不在C中)
      ldiv_t ldiv(long n, long d)====用d除n，返回(商，余数)
向量算术
<valarray>
      valarray
复数算术
<complex>
      template<class T> class std::complex;

posted @ 2012-06-05 13:59 王海光阅读(1052) | 评论 (0) | 编辑收藏

C++ Queues(队列)、Priority Queues(优先队列)

C++ Queues(队列)

C++队列是一种容器适配器，它给予程序员一种先进先出(FIFO)的数据结构。
1.back() 返回一个引用，指向最后一个元素
2.empty() 如果队列空则返回真
3.front() 返回第一个元素
4.pop() 删除第一个元素
5.push() 在末尾加入一个元素
6.size() 返回队列中元素的个数

队列可以用线性表(list)或双向队列(deque)来实现(注意vector container 不能用来实现queue，因为vector 没有成员函数pop_front!)：
queue<list<int>> q1;
queue<deque<int>> q2;
其成员函数有“判空(empty)” 、“尺寸(Size)” 、“首元(front)” 、“尾元(backt)” 、“加入队列(push)” 、“弹出队列(pop)”等操作。

例：

1 int main()
2 {
3     queue<int> q;
4     q.push(4);
5     q.push(5);
6     printf("%d\n",q.front());
7     q.pop();
8 }

C++ Priority Queues(优先队列)

C++优先队列类似队列，但是在这个数据结构中的元素按照一定的断言排列有序。
1.empty() 如果优先队列为空，则返回真
2.pop() 删除第一个元素
3.push() 加入一个元素
4.size() 返回优先队列中拥有的元素的个数
5.top() 返回优先队列中有最高优先级的元素

优先级队列可以用向量(vector)或双向队列(deque)来实现(注意list container 不能用来实现queue，因为list 的迭代器不是任意存取iterator，而pop 中用到堆排序时是要求randomaccess iterator 的!)：
priority_queue<vector<int>, less<int>> pq1; // 使用递增less<int>函数对象排序
priority_queue<deque<int>, greater<int>> pq2; // 使用递减greater<int>函数对象排序
其成员函数有“判空(empty)” 、“尺寸(Size)” 、“栈顶元素(top)” 、“压栈(push)” 、“弹栈(pop)”等。

例：

1 #include <iostream>
2 #include <queue>
3 using namespace std;
4
5 class T {
6 public:
7     int x, y, z;
8     T(int a, int b, int c):x(a), y(b), z(c)
9     {
10     }
11 };
12 bool operator < (const T &t1, const T &t2)
13 {
14     return t1.z < t2.z; // 按照z的顺序来决定t1和t2的顺序
15 }
16 main()
17 {
18     priority_queue<T> q;
19     q.push(T(4,4,3));
20     q.push(T(2,2,5));
21     q.push(T(1,5,4));
22     q.push(T(3,3,6));
23     while (!q.empty())
24     {
25         T t = q.top();
26         q.pop();
27         cout << t.x << " " << t.y << " " << t.z << endl;
28     }
29     return 1;
30 }

      输出结果为(注意是按照z的顺序从大到小出队的)：
      3 3 6
      2 2 5
      1 5 4
      4 4 3

      再看一个按照z的顺序从小到大出队的例子：

1 #include <iostream>
2 #include <queue>
3 using namespace std;
4 class T
5 {
6 public:
7     int x, y, z;
8     T(int a, int b, int c):x(a), y(b), z(c)
9     {
10     }
11 };
12 bool operator > (const T &t1, const T &t2)
13 {
14     return t1.z > t2.z;
15 }
16 main()
17 {
18     priority_queue<T, vector<T>, greater<T> > q;
19     q.push(T(4,4,3));
20     q.push(T(2,2,5));
21     q.push(T(1,5,4));
22     q.push(T(3,3,6));
23     while (!q.empty())
24     {
25         T t = q.top();
26         q.pop();
27         cout << t.x << " " << t.y << " " << t.z <<  endl;
28     }
29     return 1;
30 }

      输出结果为：
      4 4 3
      1 5 4
      2 2 5
      3 3 6
      如果我们把第一个例子中的比较运算符重载为： bool operator < (const T &t1, const T &t2) { return t1.z > t2.z; // 按照z的顺序来决定t1和t2的顺序} 则第一个例子的程序会得到和第二个例子的程序相同的输出结果。

posted @ 2012-06-05 13:21 王海光阅读(49302) | 评论 (0) | 编辑收藏

仅列出标题

常用链接

留言簿(3)

随笔分类(267)

随笔档案(269)

常用链接

朋友博客

推荐博客

最新随笔

搜索

积分与排名

最新评论

阅读排行榜

评论排行榜

Linux下C++程序常用编译命令