QM
编码器原理上是一种算术编码器,但其将每个输入的符号作单个的为来输入(二进制位要么是
0
,要么是
1
),那么符号要么是
MPS
(大概率符号),要么就是
LPS
(小概率符号)。
QM
编码器需要一个模型来首先预测下一位是
0
还是
1
,然后再输入该位来实际分类。
统计模型是用来计算
LPS
的概率
Qe
的,那么
MPS
的概率就是
1-Qe
。
Qe
是
LPS
的概率,通常情况
Qe
是小于等于
0.5
的;一般是将
LPS
的区间放在
MPS
区间的上边;
A
表示整个区间。如下图:
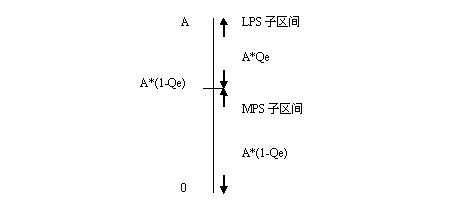
在
QM
编码器中,使用符号
C
(
code
)表示输出符号串。
QM
编码器输出的时候比普通的算术编码器简单,仅仅需要将
MPS
或
LPS
的区间下限增加到
C
中,因为这里之后两个符号。一般
QM
的编码规则是:
如果遇到一个
MPS
,
C = C+0
,
A
变成原来
MPS
的子区间了;
A = A *
(
1-Qe
)
如果碰到一个
LPS
,需要将
LPS
区间的下限(
A*
(
1-Qe
)添加到
C
中;这个时候
A
变成原来
LPS
的子区间,
A = A*Qe
。
具体规则如:
if MPS
{
C
不变;
A = A*
(
1-Qe
);
}
else //LPS
{
C = C+A*(1-Qe);
A = A*Qe;
}
重定标之后的规则:
为了使用加法、减法和移位来模拟乘除,需要在
A
小于
0.75
的时候进行重定标,保证
A
与
1
比较接近而使用加、减的操作乘法差不大。这里使用
0
到
65536
之间的整数(
16
进制的
0x0000-0x10000
)表示小数
0
到
1.5
。
那么上面的规则变为:
如果遇到一个
MPS
,
C
不变,
A
变成
MPS
的子区间;
A = A-Qe
(模拟乘法);但如果
A
小于
0.75(0x8000)
时,需要对
A
重定标,
A
加倍,
C
也加倍,直到
A
大于
0X8000
为止。
如果遇到一个
LPS
,
C
变为
C+A-Qe
(模拟原来的乘法);
A
变成
Qe
(模拟乘法);由于
LPS
的区间始终小于等于
0.5
也就是小于
0.75
,从而肯定要重定标
A
和
C
,同上。
简单表示为:
if(MPS)
{
A = A-Qe;
while(A<0X8000)
{
A <<=1;
C <<=1;
}
}
else//LPS
{
C = C+A-Qe;
A = Qe;
While(A<0X8000)
{
A<<=1;
A<<=1;
}
}
交换区间之后的规则:
由于使用加、减和移位来模拟乘法,导致有的时候
LPS
的区键会大于
MPS
的区间,这是也
QM
编码器的初始条件相违背的;因此为了运算能够继续进行,这里对
LPS
和
MPS
的区间进行交换,从而保证运算规则仍然可以进行。这个时候的上面规则是:
如果遇到一个
MPS
后;
C
仍然不变,首先将
A
设置为
MPS
的子区间(
A = A-Qe
)。这个时候需要检查是否需要重定标,检查原则同上,判断
A
是否小于
0X8000
;如果不需要重定标表示
A
大于
0X8000
,那么这个时候
MPS
肯定大于
LPS
,不需要交换区间;如果需要重定标,检查
A
是否小于
LPS
的区间
Qe
,如果小,表示需要交换区间;交换区间相当于取
LPS
的子区间,那么这个时候需要将
LPS
的区间下限输出到
C
中,从而在解码的时候做同样的操作。
如果遇到一个
LPS
后;首先将
A
先设置为
MPS
的子区间(
A = A-Qe
)。按前面的推算,应该是
A
设置为
LPS
的子区间,所以这里增加了一个判断
A
是否大于
LPS
的子区间,如果大表示我们取的是一个
MPS
的区间,和当前是
LPS
的不相符,因此应该取一个区间较小的值,也就是
LPS
,那么这个时候需要将
LPS
的下限输入到
C
中,同时
A
等于
Qe
。但如果
A
小于
LPS
的子区间,表示
MPS
的区间比
LPS
的区间小,那么如果去
LPS
表示我们取了一个大概率符号的区间,那么和输入一个
LPS
的情况不相符合,所以这种情况下,就去
A
为
MPS
的区间(
A-Qe
),从而其下限是
0
,那么
C
就不改变了。不管发生什么情况,如果输入一个
LPS
符号,总是要重标的,同前面,直到
A>0x8000
为止。
简单描述如下:
if(MPS)
{
C = C+0;
A = A-Qe;
If(A<0X8000)
{
if(A<Qe)
{
C = C+A;
A = Qe;
}
}
while(A<0X8000)
{
A <<=1;
C<<=1;
};
}
else//LPS
{
A = A-Qe;
If(A>=Qe)
{
C = C+A;
A = Qe;
}
while(A<0X8000)
{
A <<=1;
C<< =1;
};
}