Comlement and Intersection of Regular Language
Subjects to be Learned
- Complement of Regular Language
- Complement of DFA
- Intersection of Regular Languages
Contents
Complement
Let M = < Q , 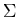 , q0 ,
, q0 , 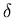 , A > be a DFA that accepts a language L. Then a DFA that accepts the complement of L, i.e.
, A > be a DFA that accepts a language L. Then a DFA that accepts the complement of L, i.e. 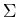 * - L, can be obtained by swapping its accepting states with its non-accepting states, that is Mc = < Q ,
* - L, can be obtained by swapping its accepting states with its non-accepting states, that is Mc = < Q , 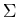 , q0 ,
, q0 , 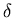 , Q - A > is a DFA that accepts
, Q - A > is a DFA that accepts 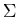 * - L .
* - L .
For example the following DFA accepts the language a+ over 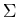 = { a , b }.
= { a , b }.
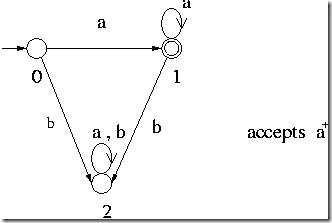
A DFA that accepts its complement is obtained from the above DFA by changing all single circles to double circles and vice versa as shown below.
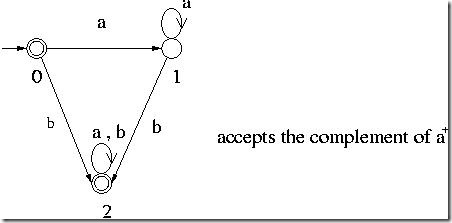
Remark 1: If we have NFA rather than DFA, we must first convert it to DFA before swapping states to get its complement.
Remark 2: Since a language is regular if and only if it is accepted by some NFA, the complement of a regular language is also regular.
Intersection of Regular Languages
Langauges are sets. Therefore all the properties of sets are inherited by languages. In particular De Morgan's law also applies to languages. By Remark 2 above, if L1 and L2 are regular languages, then their complements are regular languages. Since L1 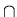 L2 =
L2 = 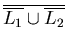 by De Morgan's law, L1
by De Morgan's law, L1 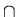 L2 is regular.
L2 is regular.
Thus summing all this up we can say that the set of regular languages over an alphabet is closed with respect to union, intersection, difference, concatenation and Kleene star operations.
Test Your Understanding of Complemnent and Intersection of FAs
Indicate which of the following statements are correct and which are not.
Click True or Fals , then Submit.