C语言是一种可移植的汇编语言,这从它的简单的语言结构可以看出来,这里面没有高级语言常见的嵌套子程序定义;没有自动的对象分配和回收;没有复杂的流程控制原语和类型定义原语。它的一切都是那么简单直接和暴露,例如它允许指针和整数之间的直接转换甚至是运算。这些都是汇编语言的特点,如果去掉针对特定处理器架构的指令集,汇编语言也就剩下这些了。
D. E. Knuth在他的名著《计算机程序设计的艺术》中使用了他自己定义的汇编语言对协同例程(coroutine)进行了比较纯粹的讨论。我们今天使用C语言来模拟协同例程,这比他的实现稍微困难一点,因为这涉及到了对C语言实现的具体技术的拆解,说白了,我们需要一些黑客的手段来取巧。这些黑客手段虽然对于大多数的C编译器都是有效的,但是从理论上讲并不是完全可以移植的。阅读本文可以得到多方面的程序设计体验,读者也许会觉得某一部分比其它部分更有趣。
虽然用C语言模拟协同例程要比使用汇编语言困难,但是并不是太难,相比于其它的高级语言,比如Pascal。不过有些非常高级的语言却直接支持某种类型的协同例程,这种类型的协同例程在实践中被认为是简化了程序的逻辑表达,故此新近的语言都试图去支持它,例如C#2。这种协同例程就是所谓的迭代子(iterator)或者生成子(generator)。我们知道,在流行的语言里面,Python是支持它的,然而和计划中的C#2一样,支持的不够好。支持协同例程方式迭代子的比较好的语言之一是Sather[1],下面我主要通过这种语言来讨论协同例程和迭代子。
当然,这里的重点并不在介绍Sather语言,只不过看看和题目相关的部分。实际上Sather已经是濒临灭绝的语言了,如今几乎找不到可以使用的编译器,像这样的语言还很多。有时候我想,一种语言想要流行,一开始必定不能有太先进的概念,在人们的使用中慢慢加入会比较让人容易适应,并误以为该语言在不断提出新概念,尽管也许十年前就已经在其它语言中实现得非常彻底了。Sather是一种过程式语言,支持面向对象的程序设计,这两点都是广为熟悉的,因此理解下面的程序片断并不会非常困难。下面是Sather语言中的循环,看起来非常易懂:
sum: INT := 0; i: INT := 1;
loop while!(i <= 10);
sum := sum + i;
i := i + 1
end;
这样子和C或Pascal的循环语句没什么太大的不同,程序的意思也是一样的。不过这里的关键字只有loop和end,while!并不是关键字,实际上它是一个迭代子,是一个协同例程。在Sather里面,迭代子是以叹号(!)结尾的,而对迭代子协同例程的创建和调用是通过loop/end循环来完成的。那么什么是协同例程呢?
子例程(subroutine)是经常使用的一种程序流程,父例程在调用子例程的时候暂时中断自身的流程,将控制转到子例程的起点,然后一直到子例程返回才继续父例程的流程。这是一种栈式的调用,就是说后进入的子例程,却要先返回。因此许多程序都是用栈来存放子例程的局部运行环境,因为当子例程返回后,这个局部的运行环境就不需要了,也就是后进先出。
然而,有些例程之间并不是父例程调用子例程这种嵌套的关系,而是并行的协同关系,当一个例程运行时,需要另外一个例程所不断产生的结果,例如两个通过管道连接的程序就是这样的关系。例程A需要数据,就把控制传递到例程B,而B产生一些数据,然后把控制返回给A,A处理完这些数据以后会需要更多的数据,于是又把控制传给B,这时并不是A重新调用B,而是恢复B刚才运行的断点,让B可以按照自己原先的流程继续运行。例程A和例程B的运行环境都需要保持,不存在谁必须先退出才能转移控制的问题。控制在这两个例程间跳来跳去,它们是协同的关系,例程B就成为例程A的协同例程,而不是子例程了。
range!(min, max: INT): INT is
i: INT := min;
loop until!(i > max);
yield i; --
i := i + 1;
end
end;
上面这个就是一个迭代子的定义,它产生从min到max的一系列整数,通过yield语句将中间结果和控制转移给主例程,再次调用同一个迭代子会使控制返回到紧接着yield语句的地方继续运行,继续产生新的中间结果。主例程通过反复调用range!来启动迭代子以及恢复迭代子的运行。而中间结果就称为迭代子的返回值。
sum: INT := 0;
loop
i: INT := range!(1, 10);
-- 当range!结束时,循环在此退出。
sum := sum + i
end;
这段程序和第一个程序的作用是一样的。我们发现while!没有了,这使得它看上去像个死循环。实际上当然不是,loop/end循环中如果存在对迭代子的调用,那么一旦其中某个迭代子结束运行,循环就会在对该迭代子的调用处退出。从下图可以看到主程序和迭代子的协同运行过程。
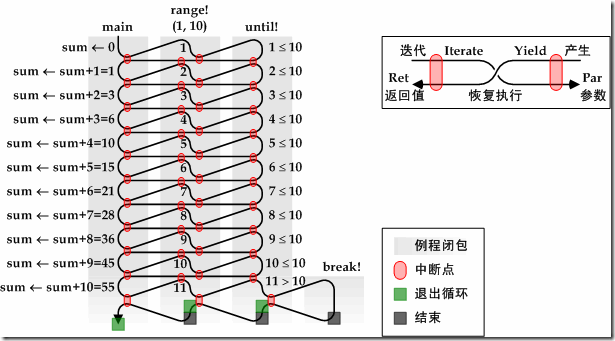
range!迭代子正是我们所描述的协同例程。迭代子通常都包含一个loop/end循环,就像range!那样,那么这个循环又是怎样退出的呢?它需要另一个迭代子until!结束的时候才能退出。不过until!迭代子也是包含循环的,最终我们需要某个不包含循环的迭代子,例如break!。
break! is end;
类似while!和until!这样的基本迭代子通常需要通过break!来退出循环。例如while!可以如下定义:
while!(pred: BOOL) is
loop
if pred then yield
else break!
end
end
end;
可以看到,while!定义中的yield后面没有返回值,它只是将控制转移回主例程。迭代子的参数并不是只在开始有用,每次通过调用恢复迭代子的运行时,主例程都可以传递不同的参数,也就是说在yield的前后,迭代子的形式参数可以代表不同的实际值。while!的唯一作用就是根据所传递的条件参数来决定是否结束运行,从而使得调用它的主例程中的循环可以根据条件结束。类似的,until!也是这个作用。它们和我们通常认为的含义完全一样,只不过更为灵活,迭代子可以出现在循环体中间,而不是必须在循环开始或结尾。
在每次恢复迭代子运行时可以传递参数(PARameter)是很有用的特性,这一点在Python语言中并不具有。我们已经看到while!和until!是怎样使用这个特性了。事实上,作为迭代子调用的参数和迭代子每次通过yield产生的返回值(RETurn value)一样,是两个互相协同运行的例程动态交换数据的渠道。表面上迭代子作为协同例程处于被动的地位,但是实际上主例程和协同例程的区别并不是那么大,主例程通过参数传递数据,协同例程通过返回值传递数据,它们几乎是对称的。
有时候,我们也构造永不结束的迭代子,或者称为生成子更合适,这种生成子通常被叫作流(stream)或者无限序列,它可以源源不断的提供某种数据。下面是一个正整数的无限序列:
positives! : INT is
i: INT := 1;
loop
yield i;
i := i+1
end
end;
使用这种迭代子的循环,要么本身是另一个无限序列,要么就需要通过其它的迭代子来退出。也就是说,我们可以在同一个循环中使用多个迭代子。从上面简单的例子中似乎看不到协同例程迭代子相对于子程序的优势,例如上图所示,流程可以很轻易转为在单一例程中执行。然而,从基本的概念上讲,迭代子可以很有效的避免两种不同操作的耦合,把数据的使用和生成分别开来。对于更为复杂的问题,利用动态生成的迭代子,则可以非常简洁的进行程序的描述。
到目前为止,迭代子看上去只是静态的一段程序。不过,在程序实际运行过程中的迭代子则类似一个线程,它是一段程序的一次运行,只不过这个线程需要在指定的地方和其它协同例程进行同步,这个指定的地方成为中断点或同步点。运行过程以及当时所在的运行环境被称为一个例程闭包,这是动态的运行对象。因此,迭代子有一个创建的过程,这个过程构造了初始的运行环境,随着例程的运行,运行环境在不断的变化。同一个迭代子描述可以生成多个运行对象,如同多个线程共享同一段代码一样。例如:
i: INT := 1;
loop
while! ( f(i) );
i := i+1;
while! ( g(i) );
i := i+2
end;
while!创建了两个迭代子。多线程确实是实现协同例程的一个选择,不过后面的例子可能会让你打消这个念头。上面我们提到了无限序列,学过数论的人都知道素数序列就是一个无限序列。现在我们就来描述这个素数生成子。首先,我们设计一个判定素数的迭代子,这个迭代子将根据依次输入的一系列整数不断产生相应的布尔判断结果。我们把这个迭代子称为sieve!,因为事实上这个实现是筛法的一个变形。sieve!的一系列输入参数符合下面三个条件:
第一个参数必须是一个素数,不妨称为x;
后面的参数必须是严格递增的,并且不能被小于x的所有素数整除;
所有满足条件2的整数都必须依次传入,没有遗漏。
在符合这三个输入参数条件的情况下,sieve!可以如下的返回判断结果:
sieve!(cand: INT): BOOL is
x: INT := cand;
yield true;
loop
if x.divides(cand) then yield false;
else yield sieve!(cand)
end
end
end;
首先,在迭代子开始,由于第一个传入的参数是素数,我们记录这个素数为x并返回真值(为了区别起见,我们用第一个参数来命名sieve!,这里也就是sieve![x]);接着,进入循环处理后来的输入参数,对于任意的后来参数y,由于严格递增的缘故,y肯定不等于x,这时如果x整除y(x|y)则y是合数,我们返回假值;否则我们递归创建和调用sieve![y]来进行进一步的判断。需要证明的是,在sieve![x]的参数满足上述条件的前提下,递归创建的sieve![y]的参数也满足这些条件。第一条是满足的,因为传入sieve![y]的是所有不能被小于或等于x的素数整除的数,而这些数以严格递增且无遗漏的方式传入sieve![x],除去那些被x整除的合数外,剩下的也是严格递增无遗漏的传给了sieve![y],所以第一次传入sieve![y]的数y必定是大于x的第一个素数;同时,我们也已经说明后面的两条也是满足的。
我们的数学归纳法还欠缺一个基础,那就是对第一个sieve!如何传递参数。非常显然,我们把从2开始的所有正整数依次传递给它就可以了。那么这个sieve![2]是不是能返回正确的判定结果呢?如果sieve![2]对于某个参数返回的话,我们可以看到返回布尔值的地方只有两个,迭代子开始的地方返回真值,我们已经证明了任何层次开始的sieve!的第一个参数都是素数;另外就是在参数被一个素数整除时返回假值。显然这两种情况都是正确的。问题是,sieve![2]会不会一去不返?这不可能,因为内层的sieve!的第一个参数严格大于外层sieve!的第一个参数(它们都是素数),而且素数是无限的,对于任一有限的正整数n,总会存在某个素数z > n,也就是说n不可能被传入sieve![z],那么判断值肯定在之前就返回了。综上所述,我们的素数无限序列就是这样的:
| primes!: INT is c: INT := 2; loop if sieve!(c) then yield c end; c := c+1 end end | quicker_primes!: INT is c: INT := 3; yield 2; loop if sieve!(c) then yield c end; c := c+2 end end |
右面那个会快一些,但是很轻微。仔细想一想就会知道我们使用了多少个协同例程,每个素数都有一个!无疑这样的判定素数的方法开销比较大,但不是在空间上的,因为即使我们用数组记录素数也需要一个萝卜一个坑,只不过例程闭包的坑大一些。这个算法的时间开销比较大,因为判定一个数n是不是素数最多只要测试小于或等于n的平方根的所有素数就可以了,这个算法却最多要测试到所有小于n的素数。如果我们使用线程来实现协同例程的话,那么操作系统就会负担很重了。我计算了一百万以内的素数,有78,498个,我真想试试操作系统的能力。尽管开销较大,但是这种程序的表达却是非常间洁的。下图示意了素数迭代子的运行过程。
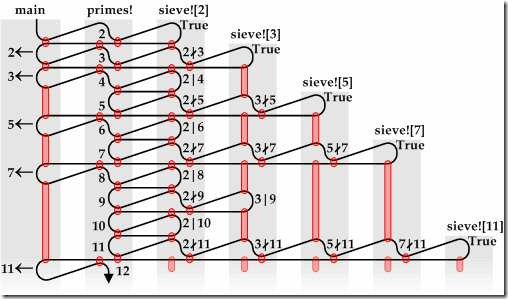
2
在缺乏原语支持的语言里,实现协同例程的关键是如何构造例程闭包。例程闭包是一个例程的代码加上在运行到某一刻时的环境,代码通常是不变的,环境则包含了该例程所用到的全局和局部的变量状态和机器状态。全局变量为所有例程所共享,它们是可以变化的,如果一个例程通过函数调用来中断运行并转移控制,那么在恢复运行后,从编译器看来是从函数调用中返回,它不会假定全局变量仍具有原来的值。对于局部于例程的变量,因为语义上它们不能被其它例程所改变,因此我们必须保证它们在中断以后可以保持不变。对于机器状态,包括断点和寄存器,也是需要保存的,它们和局部变量一起形成了例程的局部环境。因此,我们所说的例程闭包的构造主要是局部环境的保存和恢复。
C语言中有一对库函数setjmp和longjmp,它们可以用来保存断点处的机器状态,因此我们的主要任务是保存局部变量。许多的C编译器都是把局部变量放在栈上或者寄存器中,如果是后者,则在机器状态中已有保存,如果是在栈上,因为栈是各个例程所共享,则需要我们把运行时例程所用到的局部栈空间复制到另外的地方保存起来,在断点恢复以后再把栈中的数据恢复。因此,对于C编译器如何使用栈必须准确了解,我们关于这点作出如下的假定,这些假定对于许多CPU架构上的C编译器都是适用的。
栈使用的是普通的内存空间,它可以通过memcpy进行访问;
函数的调用者的局部变量、返回地址和参数在栈上的空间先于被调用函数在栈上的局部变量、返回地址和参数所占的空间;
栈空间的分配和释放都是是严格单向的(本文中假设栈是从高地址向低地址扩展,由反方向收缩,这适合于x86架构);
对一个局部变量进行取地址操作将使得编译器在栈上分配该局部变量,而不是只存放于寄存器中(这样我们可以得到例程局部栈空间中的某个位置);
对于longjmp函数,我们可以确定它使用的局部栈空间的上限。
只要我们知道例程的局部栈空间的位置(地址范围),就可以在执行setjmp保存机器状态之前利用memcpy来将局部栈中的内容保存起来。精确的范围是不需要的,我们可以保存多一些。下图展示了嵌套调用的三个例程的局部栈的关系,基于上面的假设。
| void f() { int i; void *hi = &i; g(hi); } void g(void *hi) { h(hi); } void h(void *hi) { int j; void *lo = &j; memcpy(st_save, lo, (char*)hi-(char*)lo); } | 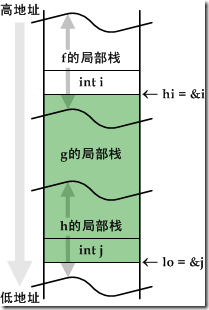
|
可以看到,通过f和h两个函数,我们取得了g的局部栈范围[2],绿色部分就是要保存和恢复的g的局部栈。保存多一点显然不碍事,但是恢复多一点又如何呢?如果我们把断点设在g里面,也就是先调用h来保存局部栈,返回g以后再转移控制到其它协同例程去,那么在g没有退回f之前,f的局部栈是不会改变的,因此恢复f局部栈的一部分没有影响;另一方面,由于h已经返回g了,h的局部栈已经没有用了,往里面写什么都没关系了。因此通过这个技巧来保存局部栈数据是正确的。不难理解,g可以代表一系列嵌套的函数调用,并不局限在一个函数:g0调用g1,g1调用g2,...,最后gN调用h。
在恢复局部栈以后需要执行longjmp来恢复机器状态(寄存器和断点),而longjmp是一个函数,它需要建立自己的局部栈,无疑我们不能让这个局部栈覆盖刚刚恢复的数据。如果假设5成立,我们对于longjmp的局部栈有上限int[L],这时可以通过一个子程序clean中的局部数组来进行判断,看看主程序restore的栈位置和要恢复的局部栈之间有没有足够空间调用longjmp,如果有,那么clean退回,由restore主程序来恢复局部栈数据并调用longjmp;如果没有,则递归调用clean,直到clean的栈完全跨越要恢复的局部栈,然后由clean来恢复局部栈及调用longjmp。这个分析如下图所示。
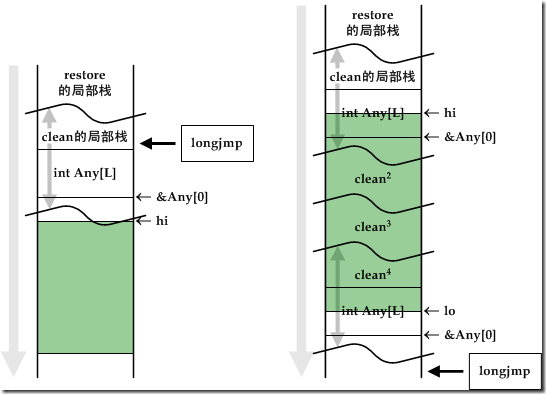
通常假设5都是成立的,因为大多数的longjmp实现只是从一个数组中恢复所有寄存器和断点,它的局部栈里几乎没有局部变量,只有参数和返回地址。当然,如果不愿意冒险去估计这个上限,那么无条件使用第二种方法也是可以的。
现在我们已经完全解决了例程局部环境的保存和恢复,下面就把这个过程正式书写出来。首先,为局部环境定义一个结构,称为局部环境块,它完全代表了一个例程闭包:
typedef int par_s, ret_s;
typedef struct _S_env env_s, *env_p;
struct _S_env {
union {
par_s Par;
ret_s Ret;
char* St_hi;
env_p Env;
} V;
env_p Co;
int Signal;
char *St_hi, *St_lo;
void *St;
int St_size;
jmp_buf Buf;
};
里面有些域尚未说明,在后面将会进行讨论。其中我们已经熟悉了St_hi和St_lo,它们储存了例程中断时的局部栈范围,St则指向可以保存局部栈的内存空间,St_size是它的大小,两次断点处的局部栈可能是不一样大的,故当St_size太小时,需要重新分配空间给St。保存和恢复局部环境的代码如下:
void Save_stack(env_p E)
{
int Any;
E->St_lo = (char*)&Any;
if ( E->St_hi-E->St_lo > E->St_size ) {
free(E->St);
E->St_size = E->St_hi-E->St_lo;
E->St = malloc(E->St_size);
}
memcpy(E->St, E->St_lo, E->St_hi-E->St_lo);
}
int Save(env_p E)
{
Save_stack(E);
return setjmp(E->Buf);
}
void Clean_restore(env_p Co)
{
env_p Any[32];
if ( (char*)&Any[1] < Co->St_lo ) {
Any[0] = Co;
memcpy(Co->St_lo, Co->St, Co->St_hi-Co->St_lo);
longjmp(Any[0]->Buf, 1);
} else if ( (char*)&Any[1] <= Co->St_hi )
Clean_restore(Co);
}
void Restore(env_p Co)
{
Clean_restore(Co);
memcpy(Co->St_lo, Co->St, Co->St_hi-Co->St_lo);
longjmp(Co->Buf, 1);
}
St_hi只能在协同例程启动时由上层调用者(也就是前面所说的f)设置,在例程运行过程中是无法得到的。这里我们假定longjmp最多使用31个机器字的栈空间,数组的第一个元素用来存放传入的参数,这是因为虽然数组的首元素跨过了需要恢复的局部栈,但是函数的参数是先于局部数组的,它可能仍处于要恢复的局部栈范围内,当局部栈恢复后,参数可能被覆盖了。这个参数指向要恢复的局部环境块,longjmp需要从中取得jmp_buf以便恢复机器状态。使用数组的一个元素并不是为了省去一个变量的声明,而是为了保证变量的位置确实不会被覆盖。
在上面的代码中有一个书写习惯,我们把正在运行的例程的局部环境块(指针)称为E(这没什么太多道理,我开始就这么用了),把将要转移过去的协同例程的局部环境块称为Co(这就有些道理了)。在后面的代码中也是保持这个习惯。
如果不保存局部栈,那么setjmp/longjmp是不能嵌在别的函数里面使用的。这对函数通常被用作异常处理,因此只是从内层函数向外层函数跳转时是有效的(这里指的是调用层次,不是书写层次,C语言中的函数没有书写层次),由于内层函数不会破坏外层函数的局部栈,因此从内往外跳不存在恢复局部栈的问题。像我们这样使用,通过调用Save来setjmp,这等于保存了子程序Save的状态,将来调用longjmp时是从外往内跳,如果不保存Save的局部栈,那么连Save的返回地址都可能丢失,通过longjmp返回到Save里面以后,很可能不知道再往什么地方返回。在其它场合使用setjmp/longjmp的时候要特别注意这个问题。
由于递归迭代子的存在,并且递归层次数量庞大,我们自然要关心栈的深度。如果我们在迭代子例程中直接启动另外一个迭代子例程,那么后面的例程的局部栈必定位于前面的之后(在这里代表更低的地址),对于sieve!这样递归的无限序列来说,栈很快就溢出了,因为预留给栈的地址空间是远远小于整个可用地址空间的。我们既然将每个协同例程的局部栈都保存了起来(在堆中),因此完全没必要受栈空间限制。各个例程可以共用同一栈地址,因为它们不会同时运行,运行之前原先的局部栈都会被恢复。如何能做到共用栈地址呢?如果所有的协同例程都由同一处启动就可以了,同样这里的同一处是指运行时的,不是书写上的。我们再次利用setjmp/longjmp,首先用setjmp静态的保存一处地方A,在需要启动协同例程时把参数存放在静态变量中,通过longjmp回到断点A继续执行,然后取出静态变量中的参数启动协同例程。如果我们不再更新断点A的机器状态,就总能回到同一个地方去,也就是总能使用同一个栈地址。递归迭代子的数量就仅受堆空间的限制了。
typedef void (*coroutine_p) (env_p);
void Setup_iter_helper(coroutine_p R, env_p E)
{
static coroutine_p R_s;
static env_p E_s;
static jmp_buf Buf;
if ( R ) {
R_s = R;
E_s = E;
longjmp(Buf, -1);
} else if ( setjmp(Buf) != 0 ) {
int Any;
E_s->V.St_hi = (char*)&Any;
R_s(E_s);
assert(0);
}
}
这段程序写得有点取巧,为的是把静态变量藏在函数中以使名字简单些。它有三个功能,首先当R=0时进行初始化,它用setjmp保存一个断点A;当R不为空时,它指向我们要启动的协同例程(上面定义了所有协同例程的原型),函数把参数转存到静态变量中后恢复断点A;断点A恢复后,函数取出静态变量中的参数启动协同例程(这里没有使用任何栈里的内容,也不能使用,因为我们没有保存这个函数的局部栈),注意由于这是启动例程的直接调用者(就是那个f),它要负责设置例程局部栈的上限,使用我们已经讨论过的技巧。局部环境结构env_s中的域V是一个联合,它的作用是传递参数,当一个协同例程启动另一个协同例程时,需要把自己的局部环境块传递给被启动者,可以看到被启动例程的局部栈上限就是这样作为参数通过启动者的局部环境块而传递的。启动者首先保存自己的局部环境,然后调用上面的函数。
env_p Setup(coroutine_p R, env_p E)
{
if ( Save(E) == 0 )
Setup_iter_helper(R, E);
return E->V.Env;
}
当控制从被启动的协同例程返回时,Setup得到一个结果,那就是被启动例程的局部环境块,利用它可以再把控制传回去。这是启动迭代子例程时启动者和被启动者的一个协议,当控制传给被启动例程后,被启动者首先必须完成局部环境块的设置,然后立即把控制返回给启动例程,以便在其需要时进行迭代,被启动的迭代子通过调用Ready来完成这个任务:
env_p Ready(env_p Co)
{
env_p E = (env_p)malloc(sizeof(env_s));
E->St = 0;
E->St_size = 0;
E->St_hi = Co->V.St_hi;
E->Signal = 0;
if ( Save(E) == 0 ) {
Co->V.Env = E;
Restore(Co);
}
if ( Is_stopped(E) )
Done(E);
return E;
}
Ready首先分配了局部环境块,初始化其中的域,然后立即保存局部环境,将块指针作为参数返回给启动者。在启动者进行首次迭代的时候,控制就会返回被启动者(我们先不要管Is_stopped,后面再讨论)。被启动者于是从调用Ready返回,得到了自己的局部环境块。
ret_s Iter(env_p E, env_p Co, par_s Par)
{
if ( Save(E) == 0 ) {
Co->Co = E;
Co->V.Par = Par;
Restore(Co);
}
return E->V.Ret;
}
虽然被启动迭代子的函数参数是启动者的局部环境块指针,但是进行迭代的例程并不一定是启动者(虽然大多数情况是,但后面也有不是的例子),因此被启动者被迭代时,其局部环境块里面有一个域Co记录了调用者的局部环境块,以便被迭代者可以将产生的结果返回给正确的调用者。调用者将迭代参数通过被迭代者的局部环境块的域V传递,同样被迭代的迭代子例程将结果放在调用者的局部环境块里面,调用者从Iter返回时便得到这个结果。
par_s Yield(env_p E, ret_s Ret)
{
if ( Save(E) == 0 ) {
E->Co->V.Ret = Ret;
Restore(E->Co);
}
return E->V.Par;
}
这便是两者之间的协同往复运行过程,我们的协同例程迭代子库也就基本完成了。还剩下什么呢?一个好的程序应该可以正常的停下来,上面的机制似乎还不足以做到。迭代子的停止有两种情况,一是自己迭代完毕,这时迭代子在自己的局部环境块中设置一个信号,表明迭代已经完成,然后把控制传递回调用者,并不断的循环等待调用者发给停止的信号:
#define ITER_S_NONE (0)
#define ITER_S_DONE (1)
#define ITER_S_STOP (2)
#define ITER_S_USER (0x00010000)
int Is_stopped(env_p E)
{
return E->Signal == ITER_S_STOP;
}
int Is_done(env_p E)
{
return E->Signal == ITER_S_DONE;
}
void Done(env_p E)
{
env_p Co;
while ( !Is_stopped(E) ) {
E->Signal = ITER_S_DONE;
Yield(E, E->V.Ret);
}
free(E->St);
Co = E->Co;
free(E);
Restore(Co);
}
接到停止信号后,协议就结束了,迭代子释放掉局部环境块,表明迭代子例程被析构,最后将控制返回给调用者。另一种情况就是调用者主动停止迭代子,这只需要在被迭代例程的局部环境块中设置停止信号:
void Stop(env_p E, env_p Co)
{
Co->Signal = ITER_S_STOP;
Iter(E, Co, E->V.Par);
}
我们看到,迭代子需要不断的等待停止信号并发送完成信号,而调用者只需要发送一次停止信号。这种非对称的协议可以避免死锁或者泄漏。由于这个协议,迭代子可能需要在每次控制返回后检测停止信号,以便及时析构,否则控制再也不会回来了,这也是上面Ready最后那句话所要做的。
调用者通过Setup启动迭代子,通过Stop停止,它们必须配对;另一方面,迭代子通过Ready创建就绪,通过Done完成析构,它们也必须配对。
不论是调用者还是迭代子都需要具有局部环境块,如果调用者本身也是一个迭代子,那么这一要求就不是问题。然而万事总有开头,迭代子总是需要启动者的。我们需要为主例程创建局部环境块:
env_p Ready_main(void *P)
{
env_p E = malloc(sizeof(env_s));
Setup_iter_helper(0, 0);
E->St = 0;
E->St_size = 0;
E->St_hi = (char*)P;
return E;
}
由于主例程没有启动者,所以局部栈上限只能自己提供,这就是上面的参数P,显然自己提供的上限不是真正的上限,有可能局部栈只被保存下面的部分,通常P指向主程序的某个局部变量。然后,我们在Ready_main这里面初始化协同例程的共用栈地址,以确保主例程可能被覆盖的局部栈部分在保存之列。这个参数是我久思不能得以消除的一个遗憾。当然与就绪配对的是完成函数:
void Done_main(env_p E)
{
free(E->St);
free(E);
}
如果主例程要直接或间接的启动迭代子,那么这些迭代子必须在这两个函数调用之间启动和停止,之后主例程当然可以再次调用这一对函数。到此,整个迭代子库就完成了,从代码看上去很简单,不是吗?下面举一些使用的例子。
3
我们先把那个素数序列翻译成C语言吧,毕竟它还算有趣。首先是判断迭代子Sieve:
void Sieve(env_p Co)
{
env_p E, Co_rec;
int X, Y;
E = Ready(Co);
X = (int)E->V.Par;
Y = (int)Yield(E, (ret_s)1);
Co_rec = Setup(&Sieve, E);
while ( !Is_stopped(E) ) {
if ( Y%X == 0 )
Y = (int)Yield(E, 0);
else
Y = (int)Yield(E, (ret_s)Iter(E, Co_rec, (par_s)Y));
}
Stop(E, Co_rec);
Done(E);
}
按照协议,首先调用了Ready,并从返回值取得自己的局部环境块,注意,在调用Ready之前不应该干太多事,尤其是分配资源,因为,如果Ready检测到停止信号就不会再返回了。从Ready返回就代表着尚未被停止,由此调用者传入的参数有效,这是第一个参数,所以是一个素数,函数通过Yield返回真值1。控制从Yield返回到迭代子以后便得到了再次迭代所传来的新参数,于是递归启动新的迭代子Co_rec,然后进入循环,根据前面讨论过的逻辑不断返回迭代结果和取得新参数,这个过程直到调用者叫停为止,在退出循环后,向递归的迭代子Co_rec发送停止消息,最后通过Done自行析构。类似的,迭代子Primes也很简单:
void Primes(env_p Co)
{
env_p E, Co_sieve;
int C = 2;
E = Ready(Co);
Co_sieve = Setup(&Sieve, E);
while ( !Is_stopped(E) ) {
if ( (int)Iter(E, Co_sieve, (par_s)C) )
Yield(E, (ret_s)C);
++C;
}
Stop(E, Co_sieve);
Done(E);
}
它启动迭代子Sieve,通过它对2以上整数依次进行判断,如果是素数就产生迭代结果,它不需要迭代参数。这几乎是原封不动的程序翻译。下面就是主例程main的定义,我们可以看到它是怎样使用迭代子的:
int main(int argc, char** argv)
{
env_p E, Co;
int N, P;
if ( argc < 2 )
return 1;
E = Ready_main(&E);
Co = Setup(&Primes, E);
N = atoi(argv[1]);
while ( (P = (int)Iter(E, Co, 0)) <= N )
printf("%d\n", P);
Stop(E, Co);
Done_main(E);
return 0;
}
与迭代子不同的是,它需要将一个局部变量的地址传给Ready_main作为局部栈的上限,这个地址肯定是在迭代子共用栈地址之上(注意条件2),因此保护它以下的部分就足够了,main启动的所有迭代子都不可能破坏这个上限之上的栈。这个程序接受一个参数N,当Primes返回的素数大于N时就停止迭代子,程序打印了不大于N的所有素数。
当一个迭代过程很简单时,通常不需要使用作为协同例程的迭代子,例如依次访问数组或链接表的所有元素。有的迭代过程较为复杂,比如中序访问二叉树的所有节点,这时迭代子的方便就显示出来了。对于复杂的数据结构,一般来说在迭代过程中是不宜对数据结构作出修改的,比如增加或删除一个节点,使用迭代子的程序应该把被迭代的数据结构当成一个快照,试图对数据结构作出修改会大大增加迭代子的复杂性,甚至消除了使用迭代子的优点。下面就是一个中序遍历二叉树的迭代子:
typedef struct _S_node node_s, *node_p;
struct _S_node {
int Val;
node_p Left, Right;
};
void Traverse(env_p Co)
{
env_p E, Co_rec;
node_p Root;
int X;
E = Ready(Co);
Root = (node_p)E->V.Par;
if ( Root == 0 )
Done(E);
Co_rec = Setup(&Traverse, E);
while ( X = (int)Iter(E, Co_rec, (par_s)Root->Left), !Is_done(Co_rec) )
Yield(E, (ret_s)X);
Stop(E, Co_rec);
Yield(E, (ret_s)Root->Val);
Co_rec = Setup(&Traverse, E);
while ( X = (int)Iter(E, Co_rec, (par_s)Root->Right), !Is_done(Co_rec) )
Yield(E, (ret_s)X);
Stop(E, Co_rec);
Done(E);
}
这个迭代子的参数(E->V.Par)是要遍历的树的根节点指针,它只在第一次传入时有用,以后传入的值都是被忽略的。这样的情形很常见,在Sather语言中有专门的关键字once来描述这样的迭代子参数,例如前面的例子range!,它所接受的参数是要生成的整数序列的上下界,这只需要传递一次。
range! (once min, max: INT): INT is ...
当然,在我们的C语言模拟库中就没有这样的设施了,一切靠自己处理。中序遍历二叉树非常简单,它首先递归迭代左子树,把迭代到的结果返回出去,然后返回根节点,最后再同样递归迭代右子树。由于二叉树并不是无限序列,所以迭代的时候要注意判断迭代子是否已经结束,这是通过迭代后判断Is_done(Co_rec)来完成的。使用这个迭代子的主程序也同样要判断这一点:
void Print_tree(node_p Root)
{
env_p E, Co;
int X;
E = Ready_main(&E);
Co = Setup(&Traverse, E);
while ( X = (int)Iter(E, Co, (par_s)Root), !Is_done(Co) )
printf("%d\n", X);
Stop(E, Co);
Done_main(E);
}
这是一个函数,它可能由main直接或间接的调用。问题出现了,如果main里面已经调用了Ready_main而尚未调用Done_main,那么就出现了嵌套的调用。我们知道在Setup_iter_helper里面设置共用栈地址的时候,机器状态被存放在静态变量中,嵌套调用是不能允许的。那么干脆只在main里面调用这对函数,因为所有的其它C函数都将从main里面调用,所以这样做是正确的,但是可能引起效率上的问题:在嵌套调用中积累起来的局部栈可能很大,特别是中间夹着的无关函数有可能在桟上定义诸如int[65536]这样的大型局部数据。故此,如果可以允许嵌套调用Ready_main/Done_main的话,就能在不同的层次指定不同的公用栈地址,只要保证在某一层中启动的迭代子也在该层结束就可以了。值得注意的是,在外层启动的迭代子不能在内层使用,因为内层所规定的主例程局部栈上限会低于外层的上限,甚至有可能低于外层规定的共有栈地址,这样一来,使用外层启动的迭代子会覆盖内层主例程没有保存的局部栈部分。
怎样支持嵌套的Ready_main调用呢?其实也不难,这是个后进先出的栈式调用模式,我们动态分配jmp_buf结构,正好利用最简单的后进先出式链接表就可以把它们串起来,这种做法是非常标准的。我们只需要修改Setup_iter_help以及Done_main就可以了。
void Setup_iter_helper(coroutine_p R, env_p E)
{
typedef struct _S_node node_s, *node_p;
struct _S_node {
node_p Next;
jmp_buf Buf;
};
static node_p Env_stack = 0;
static coroutine_p R_s;
static env_p E_s;
node_p P;
if ( R ) {
R_s = R;
E_s = E;
longjmp(Env_stack->Buf, 1);
} else if ( E == 0 ) {
P = (node_p)malloc(sizeof(node_s));
P->Next = Env_stack;
Env_stack = P;
if ( setjmp(Env_stack->Buf) != 0 ) {
int Any;
E_s->V.St_hi = (char*)&Any;
R_s(E_s);
assert(0);
}
} else {
P = Env_stack;
Env_stack = P->Next;
free(P);
}
}
void Done_main(env_p E)
{
Setup_iter_helper(0, (env_p)1);
free(E->St);
free(E);
}
这里我们增加了一个数据结构,用来存放机器状态,在每次初始化调用时分配空间并压入链接表,与此对应,我们给Setup_iter_helper增加一个新的功能,它需要在一个层次结束时把节点从链接表中弹出来释放掉,这个功能由Done_main来调用。现在,迭代子库可以支持嵌套的主例程局部环境了。
关于协同例程迭代子的应用,我再举最后一个例子[3],在这个例子里面将涉及高阶迭代子,也就是说将其它迭代子作为参数的迭代子。例如,给定两个返回值类型相同的无限序列迭代子,我们可以构造一个新的迭代子交替的产生两个序列的结果,也就是将[1,3,5,7,...]和[2,4,6,8,...]合成为[1,2,3,4,...]。这个迭代子接受两个迭代子作为参数,它称为Interleave(交替):
typedef union _U_variant variant_s, *variant_p;
union _U_variant {
int Int;
env_p Env;
variant_p Var;
coroutine_p Routine;
};
variant_p Alloc_v(int N) {return (variant_p)malloc(sizeof(variant_s)*N);}
void Free_v(variant_p P) {free(P);}
void Interleave(env_p Co)
{
env_p E;
variant_p P;
E = Ready(Co);
P = (variant_p)E->V.Par;
while (1) {
if ( Is_stopped(E) ) break;
Yield(E, (ret_s)Iter(E, P[0].Env, (par_s)P[1].Var));
if ( Is_stopped(E) ) break;
Yield(E, (ret_s)Iter(E, P[2].Env, (par_s)P[3].Var));
}
Done(E);
}
两个作为参数的迭代子是已经启动了的,它们的局部环境块和参数是通过一个参数块传递的,这是因为环境块中用于传递参数的域只有一个整数大小,我们在里面放置指向参数块的指针。上面的迭代子有4个参数,分别是第一个迭代子的环境块和参数以及第二个迭代子的环境块和参数。每个参数都是存放在上面声明的联合变体中的。使用者可以根据自己的需要声明和使用类似的变体。Interleave很简单,它交替的迭代两个迭代子并返回结果,中间不要忘了随时检查是否被停止。由于Interleave不负责启动迭代子,因此它也不负责停止它们。
假设我们有很多很多,无限多的无限序列,怎样迭代其中的元素呢?显然我们不可能迭代完一个再迭代另一个,上面的交替给我们提供了方法。如何交替无限多个无限序列呢?假定我们有一个枚举迭代子Enumerate可以生成它们的枚举序列,那么我们可以取出第一个无限序列,然后和剩下的无限多个无限序列的枚举序列进行交替,这个递归过程将可以枚举无限多个无限序列中的任何元素(当然,如果时间和空间都是足够的话),严格的说,就是任给这些序列中的元素,Enumerate都将在有限的时间内将它枚举出来。
void Enumerate(env_p Co)
{
env_p E, Co_i;
variant_p P, P_i, P_ls;
E = Ready(Co);
P = (variant_p)E->V.Par;
P_ls = (variant_p)Iter(E, P[0].Env, (par_s)(P+1));
P_i = Alloc_v(4);
P_i[0].Env = Setup(P_ls[0].Routine, E);
P_i[1].Var = P_ls+1;
P_i[2].Env = Setup(&Enumerate, E);
P_i[3].Var = P;
Co_i = Setup(&Interleave, E);
while ( !Is_stopped(E) )
Yield(E, Iter(E, Co_i, (par_s)P_i));
Stop(E, Co_i);
Stop(E, P_i[2].Env);
Stop(E, P_i[0].Env);
Free_v(P_i);
Done(E);
}
Enumerate接受一个无限序列的迭代子作为参数(P[0].Env),这个迭代子本身还可能有其它的参数,Enummerate将这些参数原封不动传给它(P[1],P[2],...)。首先Enumerate利用这个迭代子迭代出一个无限序列(P_ls[0].Routine),然后启动这个序列,这个序列可能有其它参数(P_ls[1],P_ls[2],...)。由于迭代子已经迭代过一次,因此再迭代就会返回下一个无限序列。于是Enumerate递归的启动自身来准备枚举剩下所有无限序列的元素。Enumerate将这两个启动好的迭代子交给Interleave进行交替,然后不断将Interleave的迭代结果返回出去。
好了,现在可以准备使用Enumerate迭代子了。首先需要构造无限序列的迭代子,哪里来呢?一个整数无限序列和另一个整数无限序列的笛卡尔乘积就是无限多个的整数对无限序列,比如之前定义的Positives×Primes。为了产生整数对的无限序列,我们需要一个配对迭代子,它把一个整数和一个无限序列中的所有整数配对:
void Pairs(env_p Co)
{
env_p E, Co_l;
variant_p P, P_ints;
E = Ready(Co);
P = (variant_p)E->V.Par;
P_ints = Alloc_v(2);
P_ints[0].Int = P[0].Int;
Co_l = Setup(P[1].Routine, E);
while ( !Is_stopped(E) ) {
P_ints[1].Int = (int)Iter(E, Co_l, (par_s)0);
Yield(E, (ret_s)P_ints);
}
Stop(E, Co_l);
Free_v(P_ints);
Done(E);
}
由于Pairs的迭代结果是一对整数,所以要通过参数块来返回。Pairs接受两个参数,一个是整数(P[0].Int),另一个是尚未启动的无限序列(P[1].Routine),它启动这个无限序列,并不断的将迭代结果与第一个整数配对返回。它实现了一个数的集合和一个无限序列的笛卡尔乘积。
于是,无限序列和无限序列的笛卡儿乘积Lists也可以定义了,它被表示成无限序列的无限序列,它接受两个无限序列,启动其中一个来不断生成配对的第一个整数。Lists每迭代一次就可以返回一个未启动的Pairs,这正是Enumerate所需要的:
void Lists(env_p Co)
{
env_p E, Co_l;
variant_p P, P_ls;
E = Ready(Co);
P = (variant_p)E->V.Par;
Co_l = Setup(P[0].Routine, E);
P_ls = Alloc_v(3);
P_ls[0].Routine = &Pairs;
P_ls[2].Routine = P[1].Routine;
while ( !Is_stopped(E) ) {
P_ls[1].Int = (int)Iter(E, Co_l, (par_s)0);
Yield(E, (ret_s)P_ls);
}
Free_v(P_ls);
Stop(E, Co_l);
Done(E);
}
最后我们把Lists交给Enumerate去枚举:
int main(int argc, char **argv)
{
env_p E, Co_e;
variant_p P_e, P_ints;
int i, N;
if ( argc < 2 )
return 1;
E = Ready_main(&E);
P_e = Alloc_v(3);
P_e[1].Routine = &Positives;
P_e[2].Routine = &Primes;
Co_e = Setup(&Enumerate, E);
P_e[0].Env = Setup(&Lists, E);
for ( i = 0, N = atoi(argv[1]); i < N; ++i ) {
P_ints = (variant_p)Iter(E, Co_e, (par_s)P_e);
printf("(%d, %d)\n", P_ints[0].Int, P_ints[1].Int);
}
Stop(E, P_e[0].Env);
Stop(E, Co_e);
Free_v(P_e);
Done_main(E);
return 0;
}
这个程序输出Enumerate无限序列的前N个元素(N由命令行参数指定)。它首先启动Enumerate(Co_e)和Lists(P_e[0].Env),然后把Lists和它的参数传给Enumerate去迭代,上面的参数设置过程可能看上去比较混乱,实际上它是这个意思:
Iter Enumerate Lists Positives Primes
运行的结果也是很有意思的,第一行首先被交替,所以出现的频率最高,越往后面的行交替的机会越少,少到什么程度呢?第M行的第一个元素出现在Enumerate无限序列的第2M-1个位置,例如第17行的第一个元素(17,2)将出现在第65536位。关于这个结论,不难从Enumerate和Interleave的算法中推导出来。如下图所示,这些无限序列可以组成一棵完全二叉树,位于上面的一行的元素是下面一行相应元素的子节点,而枚举的顺序正如同中序遍历这棵无限的二叉树。
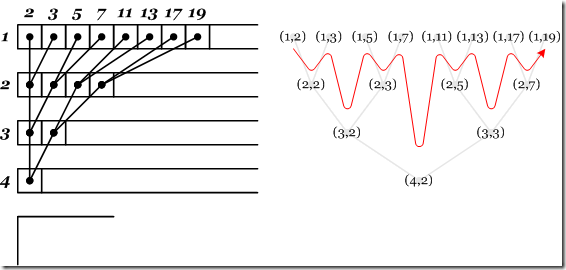
注意从4到19这条线,如果我们把整个图再往下延展的话,将画出一条对数曲线的包络线,从这一方面也知道,这种枚举方法往右上数得太快,往下数太慢。熟悉数学的人都知道另外一种对角线枚举法,这个迭代子的构造更为容易,一个想法就是,当知道紧跟下面的一行输出了该行一个元素以后,这上面的一行也要输出本行的一个元素:
void Diagonal(env_p Co)
{
env_p E, Co_ls, Co_rec;
variant_p P, P_ls;
E = Ready(Co);
P = (variant_p)E->V.Par;
P_ls = (variant_p)Iter(E, P[0].Env, (par_s)(P+1));
Co_ls = Setup(P_ls[0].Routine, E);
Co_rec = Setup(&Diagonal, E);
E->Signal = ITER_S_USER;
do {
if ( E->Signal == ITER_S_USER ) {
E->Signal = ITER_S_NONE;
E->Co->Signal = ITER_S_USER;
Yield(E, (ret_s)Iter(E, Co_ls, (par_s)(P_ls+1)));
} else
Yield(E, (ret_s)Iter(E, Co_rec, (par_s)P));
} while ( !Is_stopped(E) );
Stop(E, Co_rec);
Stop(E, Co_ls);
Done(E);
}
这里Diagonal首先输出本行的一个元素,然后递归的输出后面的那些行的元素,当紧跟下面的一行通过Signal域通知这次迭代的结果是属于该行时,Diagonal就迭代本行一次,然后同样的通知上面一行。这段程序并不难懂,这里就简而带过了。
最后这个例子实际上颇为复杂,最多时我们同时使用了Lists、Enumerate、Interleave、Pairs、Positives、Primes以及Sieve共7种迭代子,其中几个还是递归迭代子,可以想象程序运行起来同时存在多少的协同例程。协同例程迭代子为我们提供了非常有力的程序设计方式,它的思想方法和函数式语言的函数闭包(function closure),延续(continuation)有直接的对应,有兴趣的读者可以进一步去研究。本文主要讨论协同例程迭代子的概念,以及如何利用编译器的特点在C语言中模拟它。我写这个文章的动机是听说C#2将引进迭代子的语言支持,我希望这一改进能让更多的程序员可以实践丰富多彩的程序设计思想。选择C语言来模拟是因为它的简单,不用去考虑其它语言较为复杂的控制语义,例如C++的异常处理和自动析构函数。这可以使我得到更简洁的程序。
本文中的保存和恢复局部栈的技术参考了'A Portable C++ Library for Coroutine Sequencing'一文中的实现,不过进行了相应的简化;而例子部分则参考了函数式程序设计的教材。在设计迭代子C库的过程中笔者也遇到很多问题,不过一一解决起来还是非常有趣的。有时候我想,简单的程序写出来可能很长,而复杂的程序可能很短,程序中蕴涵的信息似乎不能用字节数来衡量,然而,我们却正在这么做。
这个协同例程库现在只适用于从高地址向低地址分配栈空间的机器,对Save_stack、Restore和Clean_restore稍作修改就可以适用于另一种方向分配栈空间的机器,甚至可以做到两种机器通用。文中提及的C程序的源代码可以通过gcc3或msvc6的编译,可以使用-O2优化编译。但是gcc的-O3优化编译则会导致程序崩溃,这也许是-O3会使编译器inline展开函数,失去了函数的局部栈,令文中保存局部栈的技巧失效。
参考文献
[1] Benedict Gomes, David Stoutamire, Boris Vaysman, Holger Klawitter(1996): A Language Manual For Sather 1.1, Online Material.
[2] Keld Helsgaun: A Portable C++ Library for Coroutine Sequencing, Online Material.
[3] L. C. Paulson (1996): ML for the Working Programmer, 2nd Edition, Cambridge University Pr