Something about the matrix
HOJ 2255 Not Fibonacci
题目大意:给出一个类似于Fibonacci的递推关系式f(n) = p * f(n-1) + q * f(n - 2).求出
我的做法:根据S(n)和f(n)的递推来构造一个5阶的矩阵:

这样求方阵的n次幂的第一行与初始列向量的乘积再加和即可得到结果。
总结:锻炼递推啊。。
Code:
1 #include <iostream>
#include <iostream>
2 #include <map>
#include <map>
3 #include <vector>
#include <vector>
4 #define N 6
#define N 6
5 using namespace std;
using namespace std;
6 struct matrix
struct matrix
7

 {
{
8 long long m[N][N];
long long m[N][N];
9 }E,S;
}E,S;
10 matrix multiply(matrix x, matrix y, long long mod)
matrix multiply(matrix x, matrix y, long long mod)
11

 {
{
12 matrix tmp;
matrix tmp;
13 int i, j, k;
int i, j, k;
14 for(i = 0; i < 5; i++)
for(i = 0; i < 5; i++)
15 for(j = 0; j < 5; j++)
for(j = 0; j < 5; j++)
16

 {
{
17 tmp.m[i][j] = 0;
tmp.m[i][j] = 0;
18 for(k = 0; k < 5; k++)
for(k = 0; k < 5; k++)
19

 {
{
20 tmp.m[i][j] = ((tmp.m[i][j] + x.m[i][k] * y.m[k][j] % mod) + mod) % mod;
tmp.m[i][j] = ((tmp.m[i][j] + x.m[i][k] * y.m[k][j] % mod) + mod) % mod;
21 }
}
22 }
}
23 return tmp;
return tmp;
24 }
}
25 matrix mamod(matrix P, long long b, long long mod)
matrix mamod(matrix P, long long b, long long mod)
26

 {
{
27 matrix t = E,y = P;
matrix t = E,y = P;
28 while (b)
while (b)
29

 {
{
30 if (b & 1)
if (b & 1)
31 t = multiply(t, y, mod);
t = multiply(t, y, mod);
32 y = multiply(y, y, mod);
y = multiply(y, y, mod);
33 b>>=1;
b>>=1;
34 }
}
35 return t;
return t;
36 }
}
37 long long a, b, p, q, s, e;
long long a, b, p, q, s, e;
38 long long Mod = 10000000;
long long Mod = 10000000;
39
40 long long cal(long long n)
long long cal(long long n)
41

 {
{
42 if(n == 1)
if(n == 1)
43 return a + b;
return a + b;
44 if(n == 0)
if(n == 0)
45 return a;
return a;
46 if(n < 0)
if(n < 0)
47 return 0;
return 0;
48 matrix ret = mamod(S, n - 1, Mod);
matrix ret = mamod(S, n - 1, Mod);
49
50 long long res = 0;
long long res = 0;
51
 long long t[5] =
long long t[5] =  {a + b, a, b, a, 1};
{a + b, a, b, a, 1};
52 for(int i(0); i < 5; i++)
for(int i(0); i < 5; i++)
53 res = ((res + t[i] * ret.m[0][i] % Mod) % Mod + Mod) % Mod;
res = ((res + t[i] * ret.m[0][i] % Mod) % Mod + Mod) % Mod;
54 return res;
return res;
55 }
}
56 int main()
int main()
57

 {
{
58 int test;
int test;
59 scanf("%d", &test);
scanf("%d", &test);
60 for(int i(0); i < 5; i++)
for(int i(0); i < 5; i++)
61 for(int j(0); j < 5; j++)
for(int j(0); j < 5; j++)
62 E.m[i][j] = i == j ? 1 : 0;
E.m[i][j] = i == j ? 1 : 0;
63
64 while(test--)
while(test--)
65

 {
{
66 scanf("%lld %lld %lld %lld %lld %lld", &a, &b, &p, &q, &s, &e);
scanf("%lld %lld %lld %lld %lld %lld", &a, &b, &p, &q, &s, &e);
67
68 memset(S.m, 0, sizeof(S.m));
memset(S.m, 0, sizeof(S.m));
69 S.m[1][0] = S.m[3][2] = S.m[4][4] = 1;
S.m[1][0] = S.m[3][2] = S.m[4][4] = 1;
70 S.m[0][1] = p + q;
S.m[0][1] = p + q;
71 S.m[0][2] = p;
S.m[0][2] = p;
72 S.m[2][2] = p;
S.m[2][2] = p;
73 S.m[2][3] = q;
S.m[2][3] = q;
74 S.m[0][4] = a * (1 - p) + b;
S.m[0][4] = a * (1 - p) + b;
75 printf("%lld\n", ((cal(e) - cal(s - 1)) % Mod + Mod ) % Mod);
printf("%lld\n", ((cal(e) - cal(s - 1)) % Mod + Mod ) % Mod);
76 }
}
77 return 0;
return 0;
78 }
}
HOJ 2471 Learning English
题目大意:给出一些长度为2的单词集合S,问可以构造出多少个不同的单词,而且这些单词中的每两个相邻字母构成的2长度单词必须在S中。并给定所求单词的长度上限。
我的做法:问题可以转化为求长为L的通道的条数,每个字母为一个顶点,而且要将这些长度的数目加起来,可以构造矩阵,A为邻接阵,即求S = A + A2 + A3 + … + Ak 然后再 求S中所有数字的和即可。
有两种方法:
1. 用分治的方法来进行二分,S = (E +A + A2 + A3 + … + Ak/2) *(E + Ak/2 )
2. 构造矩阵:
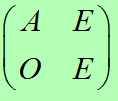
E为单位阵,O为0阵,这样求这个矩阵的n次幂右上角的矩阵则为所求的和矩阵。用快速幂可求.。
Code:
1 #include <iostream>
#include <iostream>
2 #include <map>
#include <map>
3 #include <vector>
#include <vector>
4 #define N 55
#define N 55
5 using namespace std;
using namespace std;
6 struct matrix
struct matrix
7

 {
{
8 long long m[N][N];
long long m[N][N];
9 }E,S;
}E,S;
10 matrix multiply(matrix x, matrix y, long long mod)
matrix multiply(matrix x, matrix y, long long mod)
11

 {
{
12 matrix tmp;
matrix tmp;
13 int i, j, k;
int i, j, k;
14 for(i = 0; i < 52; i++)
for(i = 0; i < 52; i++)
15 for(j = 0; j < 52; j++)
for(j = 0; j < 52; j++)
16

 {
{
17 tmp.m[i][j] = 0;
tmp.m[i][j] = 0;
18 for(k = 0; k < 52; k++)
for(k = 0; k < 52; k++)
19

 {
{
20 tmp.m[i][j] = ((tmp.m[i][j] + x.m[i][k] * y.m[k][j] % mod) + mod) % mod;
tmp.m[i][j] = ((tmp.m[i][j] + x.m[i][k] * y.m[k][j] % mod) + mod) % mod;
21 }
}
22 }
}
23 return tmp;
return tmp;
24 }
}
25 matrix mamod(matrix P, long long b, long long mod)
matrix mamod(matrix P, long long b, long long mod)
26

 {
{
27 matrix t = E,y = P;
matrix t = E,y = P;
28 while (b)
while (b)
29

 {
{
30 if (b & 1)
if (b & 1)
31 t = multiply(t, y, mod);
t = multiply(t, y, mod);
32 y = multiply(y, y, mod);
y = multiply(y, y, mod);
33 b>>=1;
b>>=1;
34 }
}
35 return t;
return t;
36 }
}
37 long long s, e;
long long s, e;
38 long long Mod = 10000000;
long long Mod = 10000000;
39 char as[213];
char as[213];
40 int main()
int main()
41

 {
{
42 int test;
int test;
43 scanf("%d", &test);
scanf("%d", &test);
44 for(int i(0); i < 52; i++)
for(int i(0); i < 52; i++)
45 for(int j(0); j < 52; j++)
for(int j(0); j < 52; j++)
46 E.m[i][j] = i == j ? 1 : 0;
E.m[i][j] = i == j ? 1 : 0;
47
48 while(test--)
while(test--)
49

 {
{
50 scanf("%lld", &s);
scanf("%lld", &s);
51 memset(S.m, 0, sizeof(S.m));
memset(S.m, 0, sizeof(S.m));
52 for (int i = 0; i < 26; i++)
for (int i = 0; i < 26; i++)
53

 {
{
54 S.m[i + 26][i + 26] = 1;
S.m[i + 26][i + 26] = 1;
55 S.m[i][i + 26] = 1;
S.m[i][i + 26] = 1;
56 }
}
57 for(int i(0); i < s; i++)
for(int i(0); i < s; i++)
58

 {
{
59 scanf("%s", as);
scanf("%s", as);
60 S.m[as[0] - 'a'][as[1] - 'a'] = 1;
S.m[as[0] - 'a'][as[1] - 'a'] = 1;
61 }
}
62 scanf("%lld", &e);
scanf("%lld", &e);
63 matrix ret = mamod(S, e, Mod);
matrix ret = mamod(S, e, Mod);
64
65 long long sum = 0;
long long sum = 0;
66 for (int i = 0; i < 26; i++)
for (int i = 0; i < 26; i++)
67

 {
{
68 for (int j = 26; j < 52; j++)
for (int j = 26; j < 52; j++)
69

 {
{
70 sum += ret.m[i][j];
sum += ret.m[i][j];
71 if (sum > 1000000)
if (sum > 1000000)
72 sum %= 1000000;
sum %= 1000000;
73 }
}
74 }
}
75 printf("%lld\n", sum - 26);
printf("%lld\n", sum - 26);
76 }
}
77 return 0;
return 0;
78 }
}
79