by Xguru
又说阶乘，这是老生常谈了吧。想都不用想，一个递归轻松搞定！
int factorial(int n)
{
if( n == 1)
return 1;
return n * factorial(n-1);
}或者你觉得递归效率没有尾递归来的好 ，大笔一挥。
long fact_iter(long product, long counter, long maxcount)
{
return (counter > maxcount) ? product : fact_iter(product*counter, counter+1, maxcount);
}
long factorial(long n)
{
return fact_iter(1, 1, n);
}
或者你看过《代码大全》上面说过：“如果为我工作的程序员用递归去计算阶乘，那么我宁愿换人。”
使用递归求阶乘速度缓慢，无法预测运行期间内存使用情况，难以理解。于是你把递归改成了循环语句。
int factorial(int n)
{
int result = 1;
for(int i = 2 ; i <= n; i++)
{
result = result * i;
}
return result;
}
当你写下这些代码的时候，会不会觉得少了些什么？
在我的32位环境上测试一下，计算到33!的时候的溢出了，于是你会说，这是int的值太小了嘛，于是你换了个long double，测试一下，什么玩意嘛这是，数再大一点的话也不行了。
那就改用链表或者数组表示吧，链表的速度就太慢了，用数组吧。
int factorial2(int n,int a[])
{
int carry;
int digit = 1;
a[0] = 1;
int temp;
for(int i = 2; i <= n; ++i)
{
for(int j = 1, carry = 0; j <= digit; ++j)
{
temp = a[j-1] * i + carry;
a[j-1] = temp % 10;
carry = temp / 10;
}
while(carry)
{
a[++digit-1] = carry % 10;
carry /= 10;
}
}
return --digit;
}
这个算法模拟手工计算的过程，将结果保存在a数组中，返回的是结果的位数
你在这个时候是不是感觉轻飘飘了呢？请暂时打住。
如果我要求一个10W以上大数的一个科学计数法的表达式呢？或者是问你，求10W 级别上的N！左边第三位的数字是多少？呃，这个是数学家的事了吧？振作精神，来挑战自我吧！真正的程序员需要的就是这种追根究底的精神。
来试试数学分析方法，James Stirling这位苏格兰数学家，280多年前就给出了这个极限式子
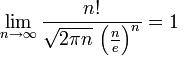
这个式子能用极快的速度求出n!的近似值，也可以使用它来无限接近准确结果。具体的介绍和证明过程在这里 或者 这里。
斯特灵级数公式
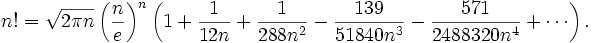
下面的代码是求大数N！科学计数法表示
struct bigNum
{
double n; //尾数
int e; //指数
};
void factorial3(struct bigNum *p,int n)
{
double logx,s,item;//s:级数的和 item:级数的每一项
int i;
logx = n* log10((double)n/E);
p->e = (int)(logx); p->n= pow(10.0, logx-p->e);
p->n *= sqrt( 2* PI* (double)n);
for (item=1.0,s=0.0,i=0;i<sizeof(a1)/sizeof(double);i++)
{
s += item * a1[i];
item /= (double)n;
}
p->n *=s;
}
下面这个是阶乘的对数的渐近展开式
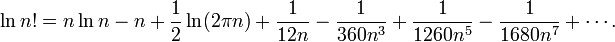
void factorial3b(struct bigNum *p,int n)
{
double logR;
double s,item;
int i;
logR=0.5*log(2.0*PI)+((double)n+0.5)*log(n)-(double)n;
for (item=1/(double)n,s=0.0,i=0;i<sizeof(a2)/sizeof(double);i++)
{
s+= item * a2[i];
item /= (double)(n)* (double)n;
}
logR+=s;
p->e = (int)( logR / log(10));//换底公式
p->n = pow(10.00, logR/log(10) - p->e);
}
要是求阶层的位数也是特别简单
double getFactorialLength(int n)
{
return (n * log(double(n)) - n + 0.5 * log(2.0 * n * PI )) / log(10.0)+1;
}
这个求出来的是位数的近似数，或者是改进一下，使用ceil函数来求出不小于给定实数的最小整数。
int getFactorialLength(int n)
{
if( n == 1 )
return 1;
else
return (int)ceil((N*log(N)-N+log(2*N*PI)/2)/log(10));
}
到此，你会不由感叹：计算机科学中最闪光，最精髓，最本质的东西还是数学！
芒德布罗集合的边界
最后用罗素的话结束这篇随笔：
Mathematics, rightly viewed, possesses not only truth, but supreme beauty — a beauty cold and austere, like that of sculpture, without appeal to any part of our weaker nature, without the gorgeous trappings of painting or music, yet sublimely pure, and capable of a stern perfection such as only the greatest art can show. The true spirit of delight, the exaltation, the sense of being more than Man, which is the touchstone of the highest excellence, is to be found in mathematics as surely as poetry.
参考资料
1.Tom M. Apostol.《数学分析, 微积分》(Mathematical Analysis)
2.Steve McConnell.《代码大全（第二版）》(CODE COMPLETE, Second Edition)
3.http://en.wikipedia.org/wiki/Stirling_approximation#History
4.http://mathworld.wolfram.com/StirlingsApproximation.html
5.http://zh.straightworldbank.com/wiki/%E6%96%AF%E7%89%B9%E6%9E%97%E5%85%AC%E5%BC%8F