Astronomers often examine star maps where stars are represented by points on a plane and each star has Cartesian coordinates. Let the level of a star be an amount of the stars that are not higher and not to the right of the given star. Astronomers want to know the distribution of the levels of the stars.
天文学家时常调查星图,星图在一个平面上表示出所有星星,而且每个星星都有笛卡尔坐标。星星的级别是不在它上面且不在它右面的星星的总数。 天文学家想知道每个星星的级别。
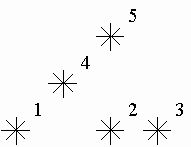
For example, look at the map shown on the figure above. Level of the star number 5 is equal to 3 (it's formed by three stars with a numbers 1, 2 and 4). And the levels of the stars numbered by 2 and 4 are 1. At this map there are only one star of the level 0, two stars of the level 1, one star of the level 2, and one star of the level 3.
举例来说,看上面的图。 5号星星的级别是3(由 1,2 和 4 号而得)。2 点和 4 号星星的级别是 1. 在这个图里只有一个级别为 0 的星星,两个级别为 1 的星星,一个级别为 2 的星星和一个级别为 3 的星星
You are to write a program that will count the amounts of the stars of each level on a given map.
你的任务是计算每个级别的星星总数
Input
The first line of the input contains a number of stars N (1<=N<=15000). The following N lines describe coordinates of stars (two integers X and Y per line separated by a space, 0<=X,Y<=32000). There can be only one star at one point of the plane. Stars are listed in ascending order of Y coordinate. Stars with equal Y coordinates are listed in ascending order of X coordinate.
第一行包含一个数 N (1<=N<=15000)。一下 N 行描述相应的星星(每行两个用空格隔开的整数 X 和 Y, 0<=X,Y<=32000)。平面上每个坐标最多只有一个星星。星星按 Y 的升序排列,Y 相等则按 X 的升序排列
Output
The output should contain N lines, one number per line. The first line contains amount of stars of the level 0, the second does amount of stars of the level 1 and so on, the last line contains amount of stars of the level N-1.
输出包含 N 行,每行一个数。第一行包含级别为 0 的星星的总数,第二行是级别为 1 的星星的总数,如此类推,最后一行是级别为 N-1 的星星的总数
Sample Input
5
1 1
5 1
7 1
3 3
5 5
Sample Output
1
2
1
1
0
分析:
此题我用的是《树状数组》,对于每个点我们先按照x升序,x同就y升序,这样我们就保
证了每个后来的点肯定是在前面点的右边,就不会影响我们后面对于每个点的计算,再有对于
每个点我们也压迫计算我它的上司(即它影响的星星),这样我们的方法就出来了:
每个点我们要做的第一步:先看它的下边有多少颗星星(不包括自己)代码:getsum(y+1)
因为我们开始从最左下的那个点开始,出来则可以判断当前星星它是属于那个级别的,那么我们
统计级别(level)那个单元即可++,再用自己的值去改变它的上司,因为虽然它不算入自己
但是对于所有它上司都将因为它增加一级,所以它要统计于它的上司范围里,代码:modify(y)
这样我们就可以统计每个星星的级别了。注意:0是十分危险的,因为lowbit(0)会死循环所以
我每个纵(y)坐标都向上升了一个格这样再上面的还是再上面,不会影响结果。
算法优越性:(1):免去了每次的向左统计,每个来的都自动统计比本身低的星星算出自己级
别,最后自己y坐标++,那么后面的只需向下看即可.(省时间)
(2):对于每个左边排序后保证了每个后来的点是不会出现再前面的前面的,保证的算法的正确性
【参考程序】://树状数组
#include<stdio.h>
#include<stdlib.h>
#include<string.h>
struct node
{
long x,y;
} point[15002];
long c[32002],level[32002];
long n;
long lowbit(long x)
{
return x^(x&(x-1));
}
void modify(long x)
{
while (x<=32001)
{
c[x]++;
x+=lowbit(x);
}
}
long getsum(long x)
{
long s=0;
while (x)
{
s+=c[x];
x-=lowbit(x);
}
return s;
}
int cmp(const void * s,const void * t)
{
node i=*(node *)s,j=*(node *)t;
if (i.x!=j.x) return i.x-j.x;
else return i.y-j.y;
}
int main()
{
scanf("%d",&n);
for (int i=1;i<=n;i++)
scanf("%d%d",&point[i].x,&point[i].y);
qsort(point+1,n,sizeof(node),cmp);
memset(c,0,sizeof(c));
memset(level,0,sizeof(level));
long k;
for (int i=1;i<=n;i++)
{
k=getsum(point[i].y+1);//防止0的坏情况
level[k]++;
modify(point[i].y+1);
}
for (int i=0;i<=n-1;i++)
printf("%d\n",level[i]);
return 0;
}