在进行文法分析的时候,通常需要检测一个单词是否在我们的单词列表里。为了提高查找和定位的速度,通常都要画出与单词列表所对应的单词查找树,其特点如下:
l 根节点不包含字母,除根节点外每一个节点都仅包含一个大写英文字母;
l 从根节点到某一节点,路径上经过的字母依次连起来所构成的字母序列,称为该节点对应的单词。单词列表中的每个词,都是该单词查找树某个节点所对应的单词;
l 在满足上述条件下,该单词查找树的节点数最少。
例:图一的单词列表对应图二的单词查找树
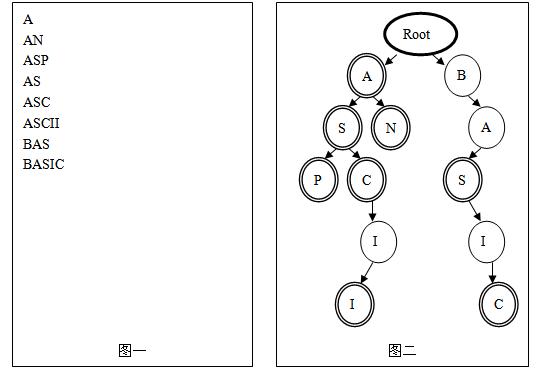
对一个确定的单词列表,请统计对应的单词查找树的节点数(包括根节点)
input:
一个单词列表,每一行仅包含一个单词和一个换行/回车符。每个单词仅由大写的英文字符组成,长度不超过63个字符。文件总长度不超过32K,至少有一行数据
output:
仅包含一个整数和一个换行/回车符。该整数为单词列表对应的单词查找树的节点数
思路:
其实就是考如何建一颗二叉树,这个二叉树每个节点都有26个孩子("A".."Z"),只要我们把所给的单词按照二叉树那样放进去即可,每放一个新的节点,ans++,最后再+1(跟节点)即是答案。
【参考程序】:
#include<string>
#include<cstdio>
#include<iostream>
#include<algorithm>
struct node
{
long a[27];
} tree[50001];
int main()
{
freopen("danci.in","r",stdin);
freopen("danci.out","w",stdout);
char s[64]={0};
memset(tree,0,sizeof(tree));
long i,j,ans;
ans=0;
while (scanf("%s",s)!=EOF)
{
j=0;
for (i=0;i<=strlen(s)-1;i++)
if (tree[j].a[s[i]-'0']==0)
{
ans++;
tree[j].a[s[i]-'0']=ans;
j=ans;
}
else j=tree[j].a[s[i]-'0'];
}
printf("%d\n",ans+1);
return 0;
}