给定4个矩形块,找出一个最小的封闭矩形将这4个矩形块放入,但不得相互重叠。所谓最小矩形指该矩形面积最小。
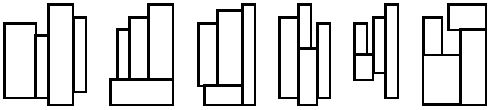
所有4个矩形块的边都与封闭矩形的边相平行,图1示出了铺放4个矩形块的6种方案。这6种方案仅只是可能的基本铺放方案。因为其它方案能由基本方案通过旋转和镜像反射得到。
可能存在满足条件且有着同样面积的各种不同的封闭矩形,你应该输出所有这些封闭矩形的边长。
INPUT FORMAT:
(file packrec.in)
共有4行。每一行用两个正整数来表示一个给定的矩形块的两个边长。矩形块的每条边的边长范围最小是1,最大是50。
OUTPUT FORMAT:
(file packrec.out)
总行数为解的总数加1。第一行是一个整数,代表封闭矩形的最小面积(子任务A)。接下来的每一行都表示一个解,由数P和数Q来表示,并且P≤Q(子任务B)。这些行必须根据P的大小按升序排列,P小的行在前,大的在后。且所有行都应是不同的。
input:
1 2
2 3
3 4
4 5
output:
40
4 10
5 8
【参考程序】:
/*
ID: XIONGNA1
PROG: packrec
LANG: C++
*/
#include<iostream>
using namespace std;
int n,s1,s2,s3,s4,d1,d2,d3,d4,area;
int ans[101][2],side[4][2];
int mul(int a,int b)
{
return a>b?a:b;
}
int MAX(int a,int b,int c,int d)
{
return mul(mul(a,b),mul(c,d));
}
void check(int w,int h)
{
if (w*h>area) return ;
if (w*h<area)
{
n=0;area=w*h;
}
if (w>h)
{
int t=w;w=h;h=t;
}
for (int i=1;i<=n;i++)
if (w==ans[i][0] && h==ans[i][1]) return ;
n++;
ans[n][0]=w;ans[n][1]=h;
}
void work()
{
int w,h,w1,w2,w3,w4,h1,h2,h3,h4;
w1=side[s1][d1]; h1=side[s1][1-d1];
w2=side[s2][d2]; h2=side[s2][1-d2];
w3=side[s3][d3]; h3=side[s3][1-d3];
w4=side[s4][d4]; h4=side[s4][1-d4];
w=w1+w2+w3+w4;
h=MAX(h1,h2,h3,h4);
check(w,h);//plan 1
w=MAX(w1+w2+w3,w4,0,0);
h=MAX(h1,h2,h3,0)+h4;
check(w,h); //plan 2
w=MAX(w1+w2,w3,0,0)+w4;
h=MAX(MAX(h1,h2,0,0)+h3,h4,0,0);
check(w,h);//plan 3
w=w1+w2+MAX(w3,w4,0,0);
h=MAX(h1,h2,h3+h4,0);
check(w,h);//plan 4 & 5
h=MAX(h2+h4,h1+h3,0,0);
if (h4>=h1+h3)
w=MAX(w2,w1+w4,w3+w4,0);
if (h3>=h2+h4)
w=MAX(w1,w2+w3,w3+w4,0);
if (h4>h3 && h4<h1+h3)
w=MAX(w1+w2,w1+w4,w3+w4,0);
if (h3>h4 && h3<h2+h4)
w=MAX(w1+w2,w2+w3,w3+w4,0);
if (h3==h4)
w=MAX(w1+w2,w3+w4,0,0);
check(w,h);
}
int main()
{
freopen("packrec.in","r",stdin);
freopen("packrec.out","w",stdout);
for (int i=0;i<=3;i++)
scanf("%d%d",&side[i][0],&side[i][1]);
area=0xFFFFFFF;n=0;
for (s1=0;s1<=3;s1++)
for (s2=0;s2<=3;s2++)
if (s1!=s2)
for (s3=0;s3<=3;s3++)
if (s1!=s3 && s2!=s3)
{
s4=6-s1-s2-s3;
for (d1=0;d1<=1;d1++)
for (d2=0;d2<=1;d2++)
for (d3=0;d3<=1;d3++)
for (d4=0;d4<=1;d4++)
work();
}
int tt;
for (int i=1;i<=n-1;i++)
for (int j=i+1;j<=n;j++)
if (ans[i][0]>ans[j][0])
{
tt=ans[i][0];ans[i][0]=ans[j][0];ans[j][0]=tt;
tt=ans[i][1];ans[i][1]=ans[j][1];ans[j][1]=tt;
}
printf("%d\n",area);
for (int i=1;i<=n;i++)
printf("%d %d\n",ans[i][0],ans[i][1]);
return 0;
}