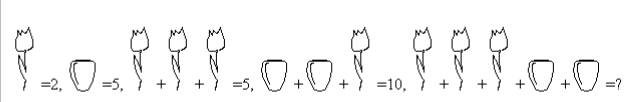
看图说话,描述题目- -
有若干类商品,然后每个商品有一定的价格,商店推出捆绑销售优惠,购买指定组合的物品可以有一定的优惠。
给出目标状态,要求花最少的钱买到指定数量的物品。
由于数据量很小,很快想到压缩状态,然后DP求从初始状态到末状态的最小花费。
这种题目我喜欢转化为图,把每个状态看作一个节点,然后求这个图上从起点到终点的最长链。对于某些看似存在后效性的状态DP中,可以采用SPFA算法,消除后效性。
贴代码
1 # include <cstdio>
2 # include <cstring>
3 using namespace std;
4 int dp[100000];
5 # define encode(n1,n2,n3,n4,n5) (((((((((n1)<<3)|(n2))<<3)|(n3))<<3)|(n4))<<3)|(n5))
6 # define getn1(sta) ((sta)>>12)
7 # define getn2(sta) (((sta)>>9)&7)
8 # define getn3(sta) (((sta)>>6)&7)
9 # define getn4(sta) (((sta)>>3)&7)
10 # define getn5(sta) ((sta)&7)
11 # define min(a,b) ((a)<(b)?(a):(b))
12 int pri[200][2],count=0;
13 int solve(int pos)
14 {
15 if(dp[pos]!=-1) return dp[pos];
16 else if(pos==0) return 0;
17 else
18 {
19 // int show1=getn1(pos),show2=getn2(pos),show3=getn3(pos),show4=getn4(pos),show5=getn5(pos);
20 int minnum=0xfffffff;
21 for(int i=count-1;i>=0;i--)
22 if(getn1(pos)-getn1(pri[i][0])>=0&&
23 getn2(pos)-getn2(pri[i][0])>=0&&
24 getn3(pos)-getn3(pri[i][0])>=0&&
25 getn4(pos)-getn4(pri[i][0])>=0&&
26 getn5(pos)-getn5(pri[i][0])>=0&&
27 solve(encode(getn1(pos)-getn1(pri[i][0]),getn2(pos)-getn2(pri[i][0]),getn3(pos)-getn3(pri[i][0]),getn4(pos)-getn4(pri[i][0]),getn5(pos)-getn5(pri[i][0])))+pri[i][1]<minnum)
28 minnum=solve(encode(getn1(pos)-getn1(pri[i][0]),getn2(pos)-getn2(pri[i][0]),getn3(pos)-getn3(pri[i][0]),getn4(pos)-getn4(pri[i][0]),getn5(pos)-getn5(pri[i][0])))+pri[i][1];
29 dp[pos]=minnum;
30 return minnum;
31 }
32 }
33 int main()
34 {
35 // FILE *in1=fopen("input.txt","r"),*in2=fopen("offer.txt","r");
36 // FILE *out=fopen("output.txt","w");
37 int num,co=1;
38 int map[1000];
39 memset(map,-1,sizeof(map));
40 memset(dp,-1,sizeof(dp));
41 scanf("%d",&num);
42 int ori=0;
43 while(num--)
44 {
45 int c,k,p;
46 scanf("%d%d%d",&c,&k,&p);
47 if(map[c]==-1) map[c]=co++;
48 c=map[c];
49 switch(c)
50 {
51 case 1:
52 pri[count][0]=encode(1,0,0,0,0);
53 ori|=encode(k,0,0,0,0);
54 break;
55 case 2:
56 pri[count][0]=encode(0,1,0,0,0);
57 ori|=encode(0,k,0,0,0);
58 break;
59 case 3:
60 pri[count][0]=encode(0,0,1,0,0);
61 ori|=encode(0,0,k,0,0);
62 break;
63 case 4:
64 pri[count][0]=encode(0,0,0,1,0);
65 ori|=encode(0,0,0,k,0);
66 break;
67 case 5:
68 pri[count][0]=encode(0,0,0,0,1);
69 ori|=encode(0,0,0,0,k);
70 break;
71 };
72 pri[count++][1]=p;
73 }
74 scanf("%d",&num);
75 while(num--)
76 {
77 int n;
78 pri[count][0]=0;
79 bool flag=true;
80 scanf("%d",&n);
81 while(n--)
82 {
83 int c,k;
84 scanf("%d%d",&c,&k);
85 if(map[c]==-1)
86 flag=false;
87 if(flag)
88 {
89 switch(map[c])
90 {
91 case 1:
92 pri[count][0]|=encode(k,0,0,0,0);
93 break;
94 case 2:
95 pri[count][0]|=encode(0,k,0,0,0);
96 break;
97 case 3:
98 pri[count][0]|=encode(0,0,k,0,0);
99 break;
100 case 4:
101 pri[count][0]|=encode(0,0,0,k,0);
102 break;
103 case 5:
104 pri[count][0]|=encode(0,0,0,0,k);
105 break;
106 };
107 }
108 }
109 scanf("%d",&n);
110 if(flag)
111 pri[count++][1]=n;
112 }
113 // for(int i=0;i<count;i++)
114 // printf("%d %d %d %d %d\n",getn1(pri[i][0]),getn2(pri[i][0]),getn3(pri[i][0]),getn4(pri[i][0]),getn5(pri[i][0]));
115 //printf("%d %d %d %d %d\n",getn1(ori),getn2(ori),getn3(ori),getn4(ori),getn5(ori));
116 printf("%d\n",solve(ori));
117 // fclose(in1);
118 //fclose(in2);
119 // fclose(out);
120 return 0;
121
122 }
123