"Help Jimmy" 是在下图所示的场景上完成的游戏。
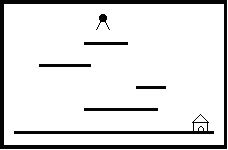
场景中包括多个长度和高度各不相同的平台。地面是最低的平台,高度为零,长度无限。
Jimmy老鼠在时刻0从高于所有平台的某处开始下落,它的下落速度始终为1米/秒。当Jimmy落到某个平台上时,游戏者选择让它向左还是向右
跑,它跑动的速度也是1米/秒。当Jimmy跑到平台的边缘时,开始继续下落。Jimmy每次下落的高度不能超过MAX米,不然就会摔死,游戏也会结束。
设计一个程序,计算Jimmy到底地面时可能的最早时间。
Input
第一行是测试数据
的组数t(0 <= t <=
20)。每组测试数据的第一行是四个整数N,X,Y,MAX,用空格分隔。N是平台的数目(不包括地面),X和Y是Jimmy开始下落的位置的横竖坐
标,MAX是一次下落的最大高度。接下来的N行每行描述一个平台,包括三个整数,X1[i],X2[i]和H[i]。H[i]表示平台的高度,X1[i]
和X2[i]表示平台左右端点的横坐标。1 <= N <= 1000,-20000 <= X, X1[i], X2[i]
<= 20000,0 < H[i] < Y <= 20000(i = 1..N)。所有坐标的单位都是米。
Jimmy的大小和平台的厚度均忽略不计。如果Jimmy恰好落在某个平台的边缘,被视为落在平台上。所有的平台均不重叠或相连。测试数据保证问题一定有解。
Output
对输入的每组测试数据,输出一个整数,Jimmy到底地面时可能的最早时间。
Sample Input
1
3 8 17 20
0 10 8
0 10 13
4 14 3
Sample Output
23
解法是这样
按照y坐标给每个区间排序,以线段端点为节点构图,每个节点最多有2条边,用线段树维护当前线段端点下方的线段。最后求最长路就可以了。
原来想简化,不要创建s和e节点,结果反而悲剧,各种漏考虑情况。。以后这类题目还是谨慎点吧。。
1 # include <cstdio>
2 # include <algorithm>
3 # include <cstring>
4 # define mid(p) ((st[p].s+st[p].e)>>1)
5 # define abs(a) ((a)>0?(a):-(a))
6 using namespace std;
7 const int N=150000;
8 int g[2005],nxt[5005],val[5005],v[5005],c,len[2005];
9 struct
10 {
11 int s,e,id;
12 }st[N];
13 struct node
14 {
15 int h,s,e;
16 }data[1005];
17 int solve(int pos)
18 {
19 if(len[pos]!=-1) return len[pos];
20 else
21 {
22 if(g[pos]==-1) return pos?0xfffffff:0;
23 else
24 {
25 len[pos]=0xfffffff;
26 for(int p=g[pos];p!=-1;p=nxt[p])
27 {
28 len[pos]=min(len[pos],solve(v[p])+val[p]);
29 }
30 return len[pos];
31 }
32 }
33 }
34 bool cmp(const node &a,const node &b)
35 {
36 return a.h<b.h;
37 }
38 void init(int s,int e,int pos=1)
39 {
40 st[pos].s=s;
41 st[pos].e=e;
42 st[pos].id=-1;
43 if(e!=s+1)
44 {
45 init(s,mid(pos),pos<<1);
46 init(mid(pos),e,(pos<<1)+1);
47 }
48 }
49 int get(int target,int pos=1)
50 {
51 if(st[pos].id!=-1) return st[pos].id;
52 else if(target>=mid(pos)) return get(target,(pos<<1)+1);
53 else return get(target,(pos<<1));
54 }
55 void insert(int s,int e,int id,int pos=1)
56 {
57 if(st[pos].s==s&&st[pos].e==e)
58 st[pos].id=id;
59 else
60 {
61 if(st[pos].id!=-1)
62 {
63 st[pos<<1].id=st[(pos<<1)+1].id=st[pos].id;
64 st[pos].id=-1;
65 }
66 if(s>=mid(pos)) insert(s,e,id,(pos<<1)+1);
67 else if(e<=mid(pos)) insert(s,e,id,pos<<1);
68 else
69 {
70 insert(s,mid(pos),id,pos<<1);
71 insert(mid(pos),e,id,(pos<<1)+1);
72 }
73 }
74 }
75 inline void addedge(int s,int e,int len)
76 {
77 v[c]=e;
78 val[c]=len;
79 nxt[c]=g[s];
80 g[s]=c++;
81 }
82 int main()
83 {
84 int test;
85 scanf("%d",&test);
86 while(test--)
87 {
88 int n,x,y,maxnum;
89 scanf("%d%d%d%d",&n,&x,&y,&maxnum);
90 for(int i=1;i<=n;i++)
91 {
92 scanf("%d%d%d",&data[i].s,&data[i].e,&data[i].h);
93 data[i].s+=20000;
94 data[i].e+=20000;
95 }
96 x+=20000;
97 data[0].h=0;
98 sort(data+1,data+n+1,cmp);
99 init(0,40001);
100 insert(0,40001,0);
101 memset(g,-1,sizeof(g));
102 c=0;
103 for(int i=1;i<=n;i++)
104 {
105 int p=get(data[i].s);
106 if(data[i].h-data[p].h<=maxnum)
107 {
108 addedge(2*i-1,p?2*p-1:0,p?abs(data[i].s-data[p].s):0);
109 addedge(2*i-1,p?2*p:0,p?abs(data[i].s-data[p].e):0);
110 }
111 p=get(data[i].e);
112 if(data[i].h-data[p].h<=maxnum)
113 {
114 addedge(2*i,p?2*p-1:0,p?abs(data[i].e-data[p].s):0);
115 addedge(2*i,p?2*p:0,p?abs(data[i].e-data[p].e):0);
116 }
117 insert(data[i].s,data[i].e+1,i);
118 }
119 {
120 int p=get(x);
121 addedge(2*n+1,p?2*p-1:0,p?abs(x-data[p].s):0);
122 addedge(2*n+1,p?2*p:0,p?abs(x-data[p].e):0);
123 }
124 memset(len,-1,sizeof(len));
125 printf("%d\n",y+solve(2*n+1));
126 }
127 return 0;
128 }
129