题意:
N个任务，每个任务有两个参数，完成需要的时间t以及因子f，现在将这些任务分组，加工每个分组前机器需要冷却时间start，完成一组任务耗时为 t + Start + (Tx + Tx+1 + ... + Tx+k)，问最少耗费的时间。
解法：
首先先解决这个问题，在这种分组数不确定的问题中，根据背包九讲中无限背包的策略，外层循环只要一层即可完成。
关键是内重循环还要枚举本组的起始位置，如果暴力的做就要N2了。
下面试图对初始的DP方程进行优化
考虑两种规划方向，第一种规划方向是从前到后
dp[i]=min{dp[k]+(dp[k]+sumt(i)-sumt(k)+start)*(sumf(i)-sumf(k))} 无比复杂的一个式子，推了N小时，在这个式子上下手似乎非常困难。。。（3个决策变量）
但是，如果换种思路，从后向前，将sumt以及sumf重新定义为最后一个任务到第i个任务的时间和和参数和，这样就简单多了。
dp[i]=min{dp[k]+(sumt(i)-sumt(k)+start)*sumf(i)}
然后很轻易能发现这个满足斜率优化的条件（2个待定决策变量，sumt(k)和dp(k)）。
关于斜率优化，一般有代数和几何两种方法。先说几何方法
令g=dp[k]+(sumt(i)-sumt(k)+start)*sumf(i)}，y=dp[k],x=sumt[k]
现在要使g最小
将式子整理下
y=sumf(i)*x+f-(start+sumt(i))*sumf(i)
将这个看做一个线性函数，目标要使得截距最小
再观察一下，斜率sumf(i)恒为正，且是随着i单调递减的，换句话说，是随着规划的过程单调递增的，而自变量x也是随着规划的过程单调递增的。我们画个图比划下
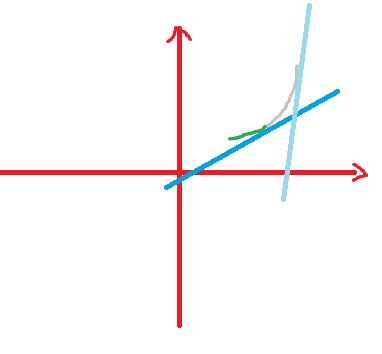
首先，我们要维护的是一个上凹线，因为凹线内部的点不会被斜率为正的直线切到。再者，我们发现最优决策就在凹线的左端。我们来观察蓝色的线，假设这个是第i阶段的决策线，灰色凹线与蓝色线切点左侧的绿色部分显然是可以丢弃的。应为在切点处截距达到最小。并且在以后的决策中（浅蓝色的线），该段同样不会有任何作用。根据以上观察，我们可以使用栈队列（很多人简称为单调队列）的数据结构。这个东西网上介绍的比较多，我就不细说了。
第二种方法就是代数法。
我看网上有一个牛写的不错，就贴过来吧- -
初始化的时候要注意，
必须在n+1的位置处加一个虚拟的状态，不能将第一个状态（即i=n的状态）作为初始状态，因为可能将所有任务仅分为一段。
代码：
1
# include <stdio.h>
2# define N 10005
3int n,start,st[N],sf[N];
4int q[N],s=-1,e=0;
5int dp[N];
6int cmp(const int a,const int b,const int k)
7
{
8
if(dp[b]-dp[a]<(long long)k*(st[b]-st[a])) return -1;
9 else if((long long)dp[b]-dp[a]==(long long)k*(st[b]-st[a])) return 0;
10 else return 1;
11
}
12int cmp1(const int y1,const int x1,const int y2,const int x2,const int y3,const int x3)
13{
14 if(((long long)y3-y2)*(x2-x1)<((long long)y2-y1)*(x3-x2)) return -1;
15 else if(((long long)y3-y2)*(x2-x1)==((long long)y2-y1)*(x3-x2)) return 0;
16 else return 1;
17}
18int main()
19{
20 int i;
21 scanf("%d%d",&n,&start);
22 for(i=0;i<n;i++)
23 scanf("%d%d",st+i,sf+i);
24 for(i=n-2;i>=0;i--)
25
{
26 st[i]+=st[i+1];
27 sf[i]+=sf[i+1];
28
}
29 q[e]=n;
30 dp[n]=0;
31 for(i=n-1;i>=0;i--)
32 {
33 while(e>=s+2&&cmp(q[s+1],q[s+2],sf[i])!=1) s++;
34 dp[i]=dp[q[s+1]]+(start+st[i]-st[q[s+1]])*sf[i];
35 while(e>=s+2&&cmp1(dp[q[e-1]],st[q[e-1]],dp[q[e]],st[q[e]],dp[i],st[i])!=1) e--;
36 q[++e]=i;
37 }
38 printf("%d\n",dp[0]);
39 return 0;
40}
41