题意: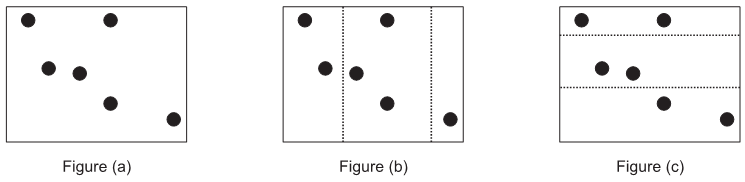
n个点,用水平线或者竖直线划分成k条,要求平均差最小,平均差为每条中点的个数减去n/k的绝对值。
解法:
首先一看就是个DP,与处理不说了,用水平扫描线、竖直扫描线将同一直线上的点压缩成一个带权值的点,然后DP
这题重要的是DP降维
观察DP方程
dp[i]=min{dp[j]+|sum[i]-sum[j]-average|}
这里就要分成两部分讨论
1、当sum[i]-sum[j]>average时
dp[i]=min{dp[j]+sum[i]-sum[j]-average}
这就是一个变量“打擂台”的问题,从前向后扫,维护一个dp[j]-sum[j]的最小值即可。
2、当sum[i]-sum[j]<average时
dp[i]=min{dp[j]+average-sum[i]+sum[j]}
这里打擂台就不行了,因为区间是移动着的。开始偷懒,直接用STL的set动态维护一个dp[j]+sum[j]的最小值。。果断TLE。。汗。。
木办法。。化简方程吧
把sum[j]看作横坐标,dp[j]看作纵坐标,转化为斜率优化问题
dp[j]=-sum[j]+sum[i]-average+dp[i]
令sum[i]-average+dp[i]=A
方程化为
dp[j]=-sum[j]+A
为了让A最小,就是找到个j,使得dp[j]+sum[j]最小,然后就是斜率优化的经典方法了,用栈队列
当dp[k]+sum[k]>dp[j]+sum[j],j>k的时候,k退栈,然后将j压栈
在栈的底端,将不符合要求的状态,即sum[i]-sum[j]>average,i>j的队头状态j给出队。这样,队头的元素就为最优值
所有元素顶多进队一次,出队一次,复杂度O(n)
总复杂度为O(k*m)
不知道怎么回事。。在POJ上死都TLE。。本机秒解,HDU500MS,可能分数类写的有点搓了。。把代码贴出来,大家看看哪里能修正修正。。。好想好想把poj给过了啊。
1 # include <cstdio>
# include <cstdio>
2 using namespace std;
using namespace std;
3 # include <vector>
# include <vector>
4 # include <algorithm>
# include <algorithm>
5 # include <utility>
# include <utility>
6 # include <functional>
# include <functional>
7 # include <map>
# include <map>
8 # include <cstring>
# include <cstring>
9 # define abs(num) ((num)>0?(num):-(num))
# define abs(num) ((num)>0?(num):-(num))
10 # define eps 1e-6
# define eps 1e-6
11 struct func
struct func
12

 {
{
13 int up,down;
int up,down;
14
 func()
func() {}
{}
15
 func(int num):up(num),down(1)
func(int num):up(num),down(1) {}
{}
16 int gcd(int a,int b)
int gcd(int a,int b)
17

 {
{
18 if(!b) return a;
if(!b) return a;
19 else return gcd(b,a%b);
else return gcd(b,a%b);
20 }
}
21 void simple()
void simple()
22

 {
{
23 int t=gcd(abs(up),abs(down));
int t=gcd(abs(up),abs(down));
24 up/=t;
up/=t;
25 down/=t;
down/=t;
26 if(down<0) up*=-1,down*=-1;
if(down<0) up*=-1,down*=-1;
27 }
}
28 func operator+(const func &pos)
func operator+(const func &pos)
29

 {
{
30 func res;
func res;
31 res.down=down*pos.down;
res.down=down*pos.down;
32 res.up=up*pos.down+pos.up*down;
res.up=up*pos.down+pos.up*down;
33 res.simple();
res.simple();
34 return res;
return res;
35 }
}
36 func operator-(const func &pos)
func operator-(const func &pos)
37

 {
{
38 func res;
func res;
39 res.down=down*pos.down;
res.down=down*pos.down;
40 res.up=up*pos.down-pos.up*down;
res.up=up*pos.down-pos.up*down;
41 res.simple();
res.simple();
42 return res;
return res;
43 }
}
44 bool operator<(const func &pos) const
bool operator<(const func &pos) const
45

 {
{
46 return up*pos.down<pos.up*down;
return up*pos.down<pos.up*down;
47 }
}
48 bool operator==(const func &pos) const
bool operator==(const func &pos) const
49

 {
{
50 return up==pos.up&&down==pos.down;
return up==pos.up&&down==pos.down;
51 }
}
52 bool operator!=(const func &pos) const
bool operator!=(const func &pos) const
53

 {
{
54 return up!=pos.up||down!=pos.down;
return up!=pos.up||down!=pos.down;
55 }
}
56 bool operator<=(const func &pos) const
bool operator<=(const func &pos) const
57

 {
{
58 return *this<pos||*this==pos;
return *this<pos||*this==pos;
59 }
}
60
61 };
};
62 int data[100000],de;
int data[100000],de;
63 func dp[10][100000];
func dp[10][100000];
64 func aver;
func aver;
65 int k;
int k;
66 int q[100000];
int q[100000];
67 func num[100000];
func num[100000];
68 struct cmp
struct cmp
69

 {
{
70 bool operator()(const pair<int,int> &a,const pair<int,int> &b) const
bool operator()(const pair<int,int> &a,const pair<int,int> &b) const
71

 {
{
72 if(dp[a.first][a.second]+func(data[a.second])!=dp[b.first][b.second]+func(data[b.second]))
if(dp[a.first][a.second]+func(data[a.second])!=dp[b.first][b.second]+func(data[b.second]))
73 return dp[a.first][a.second]+func(data[a.second])<dp[b.first][b.second]+func(data[b.second]);
return dp[a.first][a.second]+func(data[a.second])<dp[b.first][b.second]+func(data[b.second]);
74 else return a.second<b.second;
else return a.second<b.second;
75 }
}
76 };
};
77 func min(func a,func b)
func min(func a,func b)
78

 {
{
79 if(a.up*b.down<b.up*a.down) return a;
if(a.up*b.down<b.up*a.down) return a;
80 else return b;
else return b;
81 }
}
82 func solve()
func solve()
83

 {
{
84 for(int i=0;i<de;i++)
for(int i=0;i<de;i++)
85 num[i]=func(data[i]);
num[i]=func(data[i]);
86 int down=aver.up/aver.down,up=aver.up%aver.down?aver.up/aver.down+1:aver.up/aver.down;
int down=aver.up/aver.down,up=aver.up%aver.down?aver.up/aver.down+1:aver.up/aver.down;
87 for(int i=0;i<de;i++)
for(int i=0;i<de;i++)
88 if(data[i]<=down) dp[0][i]=aver-num[i];
if(data[i]<=down) dp[0][i]=aver-num[i];
89 else dp[0][i]=num[i]-aver;
else dp[0][i]=num[i]-aver;
90 for(int i=1;i<k;i++)
for(int i=1;i<k;i++)
91

 {
{
92 for(int j=0;j<de;j++)
for(int j=0;j<de;j++)
93 dp[i][j]=dp[i-1][j]+aver;
dp[i][j]=dp[i-1][j]+aver;
94 int last=-1;
int last=-1;
95 func ans=func(0xfffffff);
func ans=func(0xfffffff);
96 for(int j=0;j<de;j++)
for(int j=0;j<de;j++)
97

 {
{
98 while(data[j]-data[last+1]>=up)
while(data[j]-data[last+1]>=up)
99

 {
{
100 last++;
last++;
101 if(!last) ans= dp[i-1][last]-num[last]-aver;
if(!last) ans= dp[i-1][last]-num[last]-aver;
102 else ans=min(ans,dp[i-1][last]-num[last]-aver);
else ans=min(ans,dp[i-1][last]-num[last]-aver);
103 }
}
104 if(last!=-1)
if(last!=-1)
105 dp[i][j]=min(dp[i][j],ans+num[j]);
dp[i][j]=min(dp[i][j],ans+num[j]);
106
107 }
}
108 int s=-1,e=0;
int s=-1,e=0;
109 q[0]=0;
q[0]=0;
110 for(int j=1;j<de;j++)
for(int j=1;j<de;j++)
111

 {
{
112 //add
//add
113 while(s!=e&&dp[i-1][j]+num[j]<=dp[i-1][q[e]]+num[q[e]])
while(s!=e&&dp[i-1][j]+num[j]<=dp[i-1][q[e]]+num[q[e]])
114 e--;
e--;
115 q[++e]=j;
q[++e]=j;
116 //erase
//erase
117 while(s!=e&&data[j]-data[q[s+1]]>down) s++;
while(s!=e&&data[j]-data[q[s+1]]>down) s++;
118 if(s!=e)
if(s!=e)
119 dp[i][j]=min(dp[i][j],dp[i-1][q[s+1]]+aver-num[j]+num[q[s+1]]);
dp[i][j]=min(dp[i][j],dp[i-1][q[s+1]]+aver-num[j]+num[q[s+1]]);
120
121 }
}
122 }
}
123 return dp[k-1][de-1];
return dp[k-1][de-1];
124
125 }
}
126 int main()
int main()
127

 {
{
128 //freopen("land.in","r",stdin);
//freopen("land.in","r",stdin);
129 //freopen("ans.txt","w",stdout);
//freopen("ans.txt","w",stdout);
130 pair<int,int> d[100000];
pair<int,int> d[100000];
131 map<int,int> refer;
map<int,int> refer;
132 int n,test=1;
int n,test=1;
133 while(scanf("%d%d",&n,&k)!=EOF&&(n||k))
while(scanf("%d%d",&n,&k)!=EOF&&(n||k))
134

 {
{
135 refer.clear();
refer.clear();
136 aver.up=n;
aver.up=n;
137 aver.down=k;
aver.down=k;
138 aver.simple();
aver.simple();
139 for(int i=0;i<n;i++)
for(int i=0;i<n;i++)
140 scanf("%d%d",&d[i].first,&d[i].second);
scanf("%d%d",&d[i].first,&d[i].second);
141 for(int i=0;i<n;i++)
for(int i=0;i<n;i++)
142 refer[d[i].first]++;
refer[d[i].first]++;
143 data[0]=0;
data[0]=0;
144 de=1;
de=1;
145 for(map<int,int>::iterator i=refer.begin();i!=refer.end();i++)
for(map<int,int>::iterator i=refer.begin();i!=refer.end();i++)
146 data[de++]=(i->second);
data[de++]=(i->second);
147 for(int i=1;i<de;i++)
for(int i=1;i<de;i++)
148 data[i]+=data[i-1];
data[i]+=data[i-1];
149
150 func ans=solve();
func ans=solve();
151 refer.clear();
refer.clear();
152 for(int i=0;i<n;i++)
for(int i=0;i<n;i++)
153 refer[d[i].second]++;
refer[d[i].second]++;
154 data[0]=0;
data[0]=0;
155 de=1;
de=1;
156 for(map<int,int>::iterator i=refer.begin();i!=refer.end();i++)
for(map<int,int>::iterator i=refer.begin();i!=refer.end();i++)
157 data[de++]=(i->second);
data[de++]=(i->second);
158 for(int i=1;i<de;i++)
for(int i=1;i<de;i++)
159 data[i]+=data[i-1];
data[i]+=data[i-1];
160 ans=min(ans,solve());
ans=min(ans,solve());
161 ans.down*=k;
ans.down*=k;
162 ans.simple();
ans.simple();
163 printf("%d. %d/%d\n",test++,ans.up,ans.down);
printf("%d. %d/%d\n",test++,ans.up,ans.down);
164 }
}
165 return 0;
return 0;
166 }
}
。