本来很有目的很干脆的想写个能够支持g2d 和gui 的基本数学子库..(是内部子库,所以一切从简,事实证明这样书写还是能够增加设计效率的,当然对外子库命名规则则是遵从公共规范)
是什么我就不说了,abcd相信看命名就知道..先中场休息下...看代码吧...很直观的(除了大部分地方避免了下划线和大写命名等不和谐的命名特征所导致需要人肉分析命名功能外,没什么需要要特别注意的)

后面一段demo是关于任意连通多边形和一点的位置关系(内 or 外 or 边上)

/*  axiom.h :base::arith::axiom */


#ifndef AXIOM__

#define AXIOM__

#include "base.h"
#include "math.h"


namespace arith
{

#define PI__ 3.1415926535 
#define INFINITY__  1.79769e+308
#define MAX_PRECISION__ 1e-9

    double floor_(double x)
    {
        if(x>=0)
            return floor(x);
        else
            return floor(x)+1;
    }
    int iszero(double x)
    {
        return( x<MAX_PRECISION__)&&(x>-MAX_PRECISION__);
    }
    int formal(double& x)
    {
        if(iszero(x-floor_(x)))
        {
            x=floor_(x);
            if(x<0)x=-x;
            return 1;
        }
        return 1;
    }
    int equal(double l,double r)
    {
        if(iszero(l-r))
        {
            return 1;
        }else
        {
            return 0;
        }
    }

    class dot
    {
    public:
        double x_;
        double y_;
        dot(double _x=0,double _y=0)
        {
            x_=_x;
            y_=_y;
        }
        dot(dot & _copy)
        {
            *this=_copy;
        }
        int setx(double _x)
        {
            x_=_x;
            return 1;
        }
        int sety(double _y)
        {
            y_=_y;
            return 1;
        }
        int set(double _x,double _y)
        {
            x_=_x;
            y_=_y;
            return 1;
        }
        double getx()
        {
            return x_;
        }
        double gety()
        {
            return y_;
        }
        dot& operator = (dot & rDot)
        {
            x_=rDot.x_;
            y_=rDot.y_;
            return *this;
        }
        int operator == (dot & rDot)
        {
            return equal(x_,rDot.x_)&&equal(y_,rDot.y_);
        }
        int operator != (dot & rDot)
        {
            return (!equal(x_,rDot.x_))||(!equal(y_,rDot.y_));
        }
        int add(double dx,double dy)
        {
            x_+=dx;
            y_+=dy;
            return 1;
        }
        int mul(double l)
        {
            x_*=l;
            y_*=l;
            return 1;
        }
        int mul(double l,double r)
        {
            x_*=l;
            y_*=r;
            return 1;
        }

    };

    double def_temporary=0.0;
    class line
    {
        dot adot_;
        dot bdot_;
        double len_;
        double k_;
        double angle_;
        double getlen_()
        {
            double dx=(adot_.x_-bdot_.x_);
            double dy=(adot_.y_-bdot_.y_);
            return sqrt(dx*dx+dy*dy);
        }
        int getk_()
        {

            if(equal(adot_.x_,bdot_.x_))
            {                    

                k_=INFINITY__;/* if k doesn't exist,then we can approach infinity..*/    
                angle_=90;

            }else
            {
                k_=(bdot_.y_-adot_.y_)/(bdot_.x_-adot_.x_);

                angle_=k2a(k_);
            }

            return 1;
        }
        void renew_()
        {
            len_=getlen_();
            getk_();
            formal(adot_.x_);
            formal(adot_.y_);
            formal(bdot_.x_);
            formal(bdot_.y_);
            formal(len_);
            formal(angle_);
            formal(k_);

        }
    public:


        line(double _ax=0,double _ay=0,double _bx=0,double _by=0)
        {
            adot_.set(_ax,_ay);
            bdot_.set(_bx,_by);
            renew_();
        }

        line(dot & _adot,dot & _bdot)
        {
            adot_=_adot;
            bdot_=_bdot;
            renew_();
        }
        line(line & _copy)
        {
            *this=_copy;
        }
        /**  set  **/
        line& operator = (line & _r)
        {
            adot_=_r.adot_;
            bdot_=_r.bdot_;
            k_=_r.k_;
            len_=_r.len_;
            angle_=_r.angle_;

            return *this;
        }
        int setvector(double _ax,double _ay,double _dx,double _dy)
        {
            adot_.set(_ax,_ay);
            bdot_.set(_ax+_dx,_ay+_dy);
            renew_();
        }
        int setvector(dot & _a,double _dx,double _dy)
        {
            adot_.set(_a.x_,_a.y_);
            bdot_.set(_a.x_+_dx,_a.y_+_dy);
            renew_();
        }

        int setavector(dot & _a,double _dx,double _dy)
        {
            adot_.set(_a.x_,_a.y_);
            bdot_.set(_a.x_+_dx,_a.y_+_dy);
            renew_();
        }
        int setavector(double _ax,double _ay,double _dx,double _dy)
        {
            adot_.set(_ax,_ay);
            bdot_.set(_ax+_dx,_ay+_dy);
            renew_();
        }

        int setbvector(dot & _b,double _dx,double _dy)
        {
            adot_.set(_b.x_,_b.y_);
            bdot_.set(_b.x_+_dx,_b.y_+_dy);
            renew_();
        }
        int setbvector(double _bx,double _by,double _dx,double _dy)
        {
            bdot_.set(_bx,_by);
            bdot_.set(_bx+_dx,_by+_dy);
            renew_();
        }

        int set(double _ax=0,double _ay=0,double _bx=0,double _by=0)
        {
            adot_.set(_ax,_ay);
            bdot_.set(_bx,_by);
            renew_();
            return 1;
        }

        int set(dot & _adot,dot & _bdot)
        {
            adot_=_adot;
            bdot_=_bdot;
            renew_();
            return 1;
        }
        int setax(double _ax)
        {
            adot_.x_=_ax;
            renew_();
            return 1;
        }
        int setay(double _ay)
        {
            adot_.y_=_ay;
            renew_();
            return 1;
        }
        int setbx(double _bx)
        {
            bdot_.x_=_bx;
            renew_();
            return 1;
        }
        int setby(double _by)
        {
            bdot_.y_=_by;
            renew_();
            return 1;
        }
        int add(double _dx,double _dy)/* move a,b by vector( _dx ,_dy ) */
        {
            adot_.set(adot_.x_+_dx,adot_.y_+_dy);
            bdot_.set(bdot_.x_+_dx,bdot_.y_+_dy);
            return 1;
        }
        int adda(double _dx,double _dy)/* move a  by vector( _dx ,_dy ) */
        {
            adot_.set(adot_.x_+_dx,adot_.y_+_dy);
            renew_();
            return 1;
        }
        int addb(double _dx,double _dy)/* move b by vector( _dx ,_dy ) */
        {
            bdot_.set(bdot_.x_+_dx,bdot_.y_+_dy);
            renew_();
            return 1;
        }
        int fixa(double _x,double _y) /* fix a's position on ( _x ,_y ) and don't change the relation of a and b */
        {
            double dx=(bdot_.x_-adot_.x_);
            double dy=(bdot_.y_-adot_.y_);
            adot_.set(_x,_y);
            bdot_.set(_x+dx,_y+dy);
            renew_();
            return 1;
        }
        int fixb(double _x,double _y)/* fix b's position on ( _x ,_y ) and don't change the relation of a and b */
        {
            double dx=(adot_.x_-bdot_.x_);
            double dy=(adot_.y_-bdot_.y_);
            bdot_.set(_x,_y);
            adot_.set(_x+dx,_y+dy);
            renew_();
            return 1;
        }
        int rotb(double _angle)
        {
            double dx=(bdot_.x_-adot_.x_);
            double dy=(bdot_.y_-adot_.y_);
            double radian=c2r(dx,dy);
            double _d_radian=a2r(_angle);

            bdot_.set(adot_.getx()+len_*cos(radian+_d_radian),
                adot_.gety()+len_*sin(radian+_d_radian));
            renew_();
            return 1;
        }
        int rotb_radian(double _d_radian)
        {
            double dx=(bdot_.x_-adot_.x_);
            double dy=(bdot_.y_-adot_.y_);
            double radian=c2r(dx,dy);

            bdot_.set(adot_.getx()+len_*cos(radian+_d_radian),
                adot_.gety()+len_*sin(radian+_d_radian));
            renew_();
            return 1;
        }
        int rotb_angle(double _angle)
        {
            double dx=(bdot_.x_-adot_.x_);
            double dy=(bdot_.y_-adot_.y_);
            double radian=c2r(dx,dy);

            double _d_radian=a2r(_angle);
            bdot_.set(adot_.getx()+len_*cos(radian+_d_radian),
                adot_.gety()+len_*sin(radian+_d_radian));
            renew_();
            return 1;
        }
        int rota(double _angle)
        {
            double dx=(adot_.x_-bdot_.x_);
            double dy=(adot_.y_-bdot_.y_);
            double radian=c2r(dx,dy);

            double _d_radian=a2r(_angle);
            adot_.set(bdot_.getx()+len_*cos(radian+_d_radian),
                bdot_.gety()+len_*sin(radian+_d_radian));
            renew_();
            return 1;
        }
        int rota_radian(double _d_radian)
        {
            double dx=(adot_.x_-bdot_.x_);
            double dy=(adot_.y_-bdot_.y_);
            double radian=c2r(dx,dy);

            adot_.set(bdot_.getx()+len_*cos(radian+_d_radian),
                bdot_.gety()+len_*sin(radian+_d_radian));
            renew_();
            return 1;
        }
        int rota_angle(double _angle)
        {
            double dx=(adot_.x_-bdot_.x_);
            double dy=(adot_.y_-bdot_.y_);
            double radian=c2r(dx,dy);

            double _d_radian=a2r(_angle);
            adot_.set(bdot_.getx()+len_*cos(radian+_d_radian),
                bdot_.gety()+len_*sin(radian+_d_radian));
            renew_();
            return 1;
        }
        
        /**  get  **/
        double getax()
        {
            return adot_.x_;
        }
        double getay()
        {
            return adot_.y_;
        }
        double getbx()
        {
            return bdot_.x_;
        }
        double getby()
        {
            return bdot_.y_;
        }
        double getlen()
        {
            return len_;
        }
        double getk()
        {
            return k_;
        }
        dot geta()
        {
            return adot_;
        }
        dot getb()
        {
            return bdot_;
        }
        int bek()
        {
            return adot_.x_!=bdot_.x_;
        }
        double getangle()
        {
            return angle_;
        }

        double operator()(int _index)/* (0,1,2,3,others) = (ax,ay,bx,by,length) */
        {
            if(_index==0)
                return getax();
            else if(_index==2)
                return getay();
            else if(_index==1)
                return getbx();
            else if(_index==3)
                return getby();
            else
                return len_;
        }
        double operator()(int _aorb,int _xory)/* 0 is a or x,other is b or y */
        {
            if(_aorb==0&&_xory==0)
                return getax();
            else if(_aorb==0&&_xory!=0)
                return getay();
            else if(_aorb!=0&&_xory==0)
                return getbx();
            else if(_aorb!=0&&_xory!=0)
                return getby();
            return 1.0;
        }
        int operator ==(line & _r)
        {
            return (adot_==_r.adot_)&&(bdot_==_r.bdot_);
        }
        int operator !=(line & _r)
        {
            return (adot_!=_r.adot_)||(bdot_!=_r.bdot_);
        }
        int operator > (line & _r)
        {
            return (len_ > _r.len_);
        }
        int operator < (line & _r)
        {
            return (len_ < _r.len_);
        }
        int operator >= (line & _r)
        {
            return (len_ >= _r.len_)||(equal(len_,_r.len_));
        }
        int operator <= (line & _r)
        {
            return (len_ <= _r.len_)||(equal(len_,_r.len_));
        }
        int isalong(dot & _dot)
        {
            return isalong(_dot.x_,_dot.y_);
        }
        int isalong(double _x,double _y)/* is (_x,_y) along this line */
        {
            if(angle_==90)
            {
                if(_x==adot_.getx())
                    return 1;
                else
                    return 0;
            }
            if(equal(
                (_y-adot_.gety())-k_*(_x-adot_.getx()),0.0
                ))
                return 1;
            else
                return 0;
        }
        int iscover(dot & _dot)
        {
            return iscover(_dot.x_,_dot.y_);
        }
        int iscover(double _x,double _y)
        {
            if(!isalong(_x,_y))
                return 0;
            
            if((_x-adot_.getx())*(_x-bdot_.getx())>0)
                return 0;
            else
                return 1;
        }
        int iscross(line & _l,double &_x=def_temporary,double &_y=def_temporary)
        {
            double x,y;
            int state=getcrossdot(_l,x,y);
            
            
            if(state==2)
            {
                return state;
            }else if(state==0)
            {
                
                return 0;
            }else if(state==1)
            {
                
                _l.iscover(x,y);
                if(iscover(x,y)&&_l.iscover(x,y))
                {
                    _x=x;
                    _y=y;
                    return 1;
                }else
                {
                    return 0;
                }
            }else
            {
                return 0;
            }
        }
        int getcrossdot(line & _l,double &_x,double &_y)
        {
            if(angle_!=90&&_l.angle_!=90)
            {
                
                if(k_==_l.k_)
                {
                    if(isalong(_l.getax(),_l.getay()))
                        return 2;
                    else
                        return 0;
                }else
                {
                    double dk = k_-_l.k_;
                    _x=(_l.getay()-getay()+getax()*k_-_l.k_*_l.getax())/dk;
                    _y=_l.k_*(k_*(-_l.getay()/_l.k_+_l.getax()-getax())+getay())/(-dk);
                    return 1;
                }

            }else if(angle_==90)
            {
                if(_l.angle_==90)
                {
                    if(getax()==_l.getax())
                    {
                        return 2;
                    }else
                    {
                        return 0;
                    }
                }else
                {
                    _x=getax();
                    _y=_l.k_*(getax()-_l.getax())+_l.getay();
                    return 1;
                }
            }else /* here _l.angle_ must be 90 and angle_ must not be 90*/
            {
                    _x=_l.getax();
                    _y=k_*(_l.getax()-getax())+getay();
                    return 1;
            }
        }
        /** others  **/
        double a2r(double angle) /* angle to radian */
        {
            return (angle)*(PI__/180);
        }
        double a2k(double angle) /* angle to slope */
        {
            return tan((angle)*(PI__/180));

        }
        double r2a(double radian)/* slope to angle */
        {
            return (radian)*(180/PI__);
        }
        double a2a(double angle) /* angle to natural angle */
        {
            return ((int)floor_(angle))%360+(angle-(floor_(angle)));
        }
        double k2a(double k)
        {
            return (atan(k))*(180/PI__);
        }
        double k2r(double k)
        {
            return atan(k);
        }
    

        double c2r(double x,double y)
        {
            if(x==0&&y!=0)
                return PI__/2;
            else if(x==0&&y==0)
                return 0;
            double k=y/x;
            if(x>0&&y>=0)
            {
                return k2r(k);
            }else if(x>0&&y<0)
            {
                return k2r(k);
            }else if(x<0&&y>=0)
            {
                return (PI__+k2r(k));
            }else
            {
                return (PI__+k2r(k));
            }


        }



    };
}


#endif





接下来的demo是关于刚才讲的给出一个点,n个有序点组成的不规则连通多边形,比如: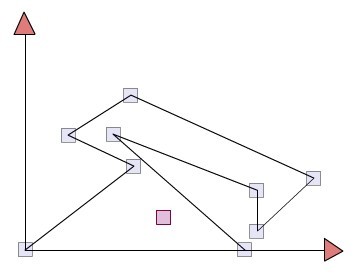

小方块代表多边形结点,连起来就是不规则连通(自身线段不相交)多边形,判断红色点是否在多边形里面.

由于是不规则多边形,不可能通过趋近的方法单纯的检测边界.

采用了以前自己重新发现的某个方法,就是奇/偶规则：

该点向任意一方向构造射线,与多边形相交次数偶数则在多边形外面,否则则在里面,当检测到是在线上,则在多边形边界上(这里默认边界也是里面).

另外要注意切边规则，也就是射线恰好切到结点处，这时候要检测是切入还是外切是很难的（相当于问题本身的递归）,除非用重构等效多边形的方法避开切到结点的问题(把被切到的多边形结点的x,y值各增加0.000000001和0.0000010203类似的方法),这里先暂时不考虑


代码如下:

void test_arith_axiom()
{
using namespace arith;
    double x ,y ;

    dot list[51],d;
    int n;
    cin>>n;
    for(int i=0;i!=n+1;i++)
    {
        cin>>x>>y;
        list[i].set(x,y);
    }
    double crossNum=0;

    line xline(x,y,x+500,y),iterline;
    for(int i=0;i!=n;i++)
    {
        if(i==n-1)
            iterline.set(list[n-1].getx(),list[n-1].gety(),list[0].getx(),list[0].gety());
        else
            iterline.set(list[i].getx(),list[i].gety(),list[i+1].getx(),list[i+1].gety());
        if(xline.iscross(iterline,x,y))
        {
            d.set(x,y);
            if(d==iterline.geta()||d==iterline.getb())
                crossNum+=0.5;
            else
                crossNum+=1;
        }
    }
    if(((int)(crossNum)%2)==1)
        cout<<"your point is in this polygon.\n";
    else
        cout<<"your point is out of this polygon.\n";

}


Input and Output:

9
0 0
2 2
1 3
2 4
4 2
3.1 0.9001
3 2
2 3
3 0
2.031 1.1
4
5
7
3
your point is in this polygon.



另外:写关于算法的代码我采取了另一种简略命名方法,考虑到对于此类代码成员方法使用频率很高:
point <=>dot,
rotateA <=> rota,
radian to angle <=>r2a
get A point <=> geta
get A point's x <=> getax
.......
.....

(每一条线有相对方向和位置,具有直线,向量,线段三重实现,所以内部约定了a,b两点)