在讲贝叶斯公式之前,我必须先提一下条件概率和全概率公式。
条件概率:设A,B是两个事件,且P(B) > 0,称
-
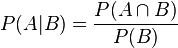
为在事件B发生的条件下,事件A发生的条件概率。
例子:袋中有7个黑球和3个白球,从中无放回地随机抽取3个球,已知其中有黑球,试求取得2个黑球1个白球的概率。
设A = {抽取的3个球有黑球};B = {取得2个黑球1个白球}。故所求事件的概率为P(B|A)。利用条件概率定义计算。此时样本空间中的样本点总数n = C(10,3),事件A包含的样本点数k1 = C(7,1) * C(3,2) + C(7,2) * C(3,1) + C(7,3) = 119,事件AB包含的样本点数k2 = C(7,2) * C(3,1) = 63.则
P(B | A) = P(BA) / P(A) = (k2 / n) / (k1 / n) = k2 / k1 = 63 / 119。
全概率:


贝叶斯:



/Files/zhuxin/概率论.pdf
posted on 2012-10-25 12:38
zhuxin 阅读(251)
评论(0) 编辑 收藏 引用 所属分类:
数学