先考虑不旋转的情况,也不考虑取模什么的,此时是一个纯粹的生成树计数问题(见zd的08年集训队论文),可以表示成一个行列式:

由于n很大,所以不能直接求解该行列式,需要对其进行化简:
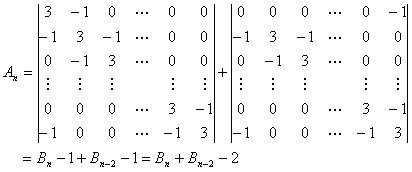
其中, 
且容易得出有关它的递推式:Bn=3Bn-1-Bn-2
于是借助矩阵乘法,就可以在O(logn)时间内,求出An的值
下面考虑旋转,此时,可以用Burnside引理,考虑每种置换下不变的方案数,旋转i时的轮换长度均为d(i)=gcd(n,i),因此该置换不变的方案数显然是Ad(i),故总方案数为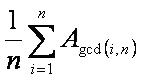
计算中,许多gcd(i,n)的值,是相同的,所以可以用欧拉函数对上式变形
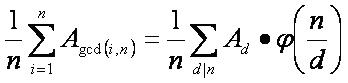
最后考虑取模问题,我们不妨先每次让它模n*m,计算每种置换下不变的方案数的和,最后直接除以n即可。由于n*m最大可以为1018,这里要用到大整数乘积取模。
#include <iostream>
#include <cstdlib>
using namespace std;
long long mo;
long long f[40][2][2],g[40][2][2];
long long mulmod(const long long &a,long long b)
{
long long res=0,tmp=a%mo;
while(b>0)
{
if (b&1)
if ((res+=tmp)>mo) res-=mo;
if ((tmp<<=1)>mo) tmp-=mo;
b>>=1;
}
return res;
}
void multi(long long a[2][2],long long b[2][2],long long c[2][2])
{
int i,j;
for(i=0;i<2;i++)
for(j=0;j<2;j++)
c[i][j]=(mulmod(a[i][0],b[0][j])+mulmod(a[i][1],b[1][j]))%mo;
}
long long detB(int n)
{
if (n==0) return 1;
int o=0,i,t=n-1;
for(i=0;t>0;i++,t>>=1)
if ((t&1)==1)
{
multi(g[o],f[i],g[o+1]);
o++;
}
return (g[o][0][0]*3%mo+g[o][1][0]*8%mo)%mo;
}
long long detA(int n)
{
if (n==1) return 1;
return (detB(n)-detB(n-2)+mo+mo-2)%mo;
}
int euler(int n)
{
int ans=1,i;
for(i=2;i*i<=n;i++)
if (n%i==0)
{
ans*=i-1; n/=i;
while(n%i==0)
{ ans*=i; n/=i; }
}
if (n>1) ans*=n-1;
return ans;
}
int main(void)
{
int n,m,i,d,res;
long long sum;
g[0][0][0]=1; g[0][0][1]=0;
g[0][1][0]=0; g[0][1][1]=1;
while(scanf("%d%d",&n,&m)!=EOF)
{
mo=(long long)(n)*m;
f[0][0][0]=0; f[0][0][1]=mo-1;
f[0][1][0]=1; f[0][1][1]=3;
for(i=1;i<30;i++)
multi(f[i-1],f[i-1],f[i]);
sum=0;
for(i=1;i*i<=n;i++)
{
if (n%i!=0) continue;
d=i;
sum=(sum+mulmod(detA(d),euler(n/d)))%mo;
if (i*i==n) break;
d=n/i;
sum=(sum+mulmod(detA(d),euler(n/d)))%mo;
}
res=sum/n;
printf("%d\n",res);
}
return 0;
}
posted on 2010-10-03 21:56
zxb 阅读(985)
评论(7) 编辑 收藏 引用