这里,可以借助kmp算法,它的本质是按顺序比较
我们考虑两个字符串A,B
A[1],A[2],…,A[k]与B[1],B[2],…,B[k]匹配条件:
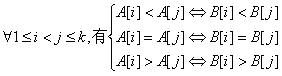
若A[1],A[2],…,A[k-1]与B[1],B[2],…,B[k-1]匹配,则加上A[k]与B[k]仍然匹配的条件是:
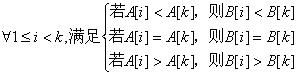
必须在与k无关的时间复杂度内完成该操作
然而,由于A[1],A[2],…,A[k-1]与B[1],B[2],…,B[k-1]已经匹配,可以简化比较操作
考虑到字符集很小(不超过25),我们可以定义以下几个变量:
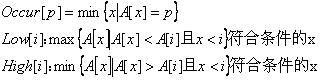
Occur[p],Low[i],High[i]可能不存在,若存在则取最小的符合条件的x
则A[1],A[2],…,A[k-1]与B[1],B[2],…,B[k-1]匹配,加上A[k]与B[k]仍然匹配的条件可简化为:
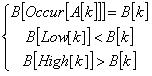
接下来就可以用O(SK)时间内预处理求出Occur[p],Low[i],High[i],然后套用kmp算法,总时间复杂度为O(N+SK),具体实现时要注意Occur[p],Low[i],High[i]不存在的情况。
当然,若用并查集来优化预处理,可以把总时间复杂度降为接近线性。
#include <iostream>
#include <cstdlib>
using namespace std;
int occur[30],low[25000],high[25000],pre[25000];
int a[25000],b[100000];
int ans[100000];
bool cmp(int *a,int *b,int k)
{
if (b[occur[a[k]]]!=b[k]) return false;
if ((low[k]>=0)&&b[low[k]]>=b[k]) return false;
if ((high[k]>=0)&&b[high[k]]<=b[k]) return false;
return true;
}
int main(void)
{
int n,k,s;
int i,j,m;
scanf("%d%d%d",&n,&k,&s);
for(i=0;i<n;i++)
scanf("%d",b+i);
for(i=1;i<=s;i++)
occur[i]=-1;
occur[0]=occur[s+1]=-2;
for(i=0;i<k;i++)
{
scanf("%d",a+i);
if (occur[a[i]]==-1)
occur[a[i]]=i;
for(j=a[i]-1;occur[j]==-1;j--);
low[i]=occur[j];
for(j=a[i]+1;occur[j]==-1;j++);
high[i]=occur[j];
}
pre[0]=-1;
j=-1;
for(i=1;i<k;i++)
{
while(j>=0&&!cmp(a,a+(i-j-1),j+1)) j=pre[j];
if (cmp(a,a+(i-j-1),j+1)) j++;
pre[i]=j;
}
j=-1; m=0;
for(i=0;i<n;i++)
{
while(j>=0&&!cmp(a,b+(i-j-1),j+1)) j=pre[j];
if (cmp(a,b+(i-j-1),j+1)) j++;
if (j+1==k)
{
ans[m++]=i-j+1;
j=pre[j];
}
}
printf("%d\n",m);
for(i=0;i<m;i++)
printf("%d\n",ans[i]);
return 0;
}
posted on 2010-10-06 14:24
zxb 阅读(1895)
评论(4) 编辑 收藏 引用