http://61.187.179.132:8080/JudgeOnline/showproblem?problem_id=2005这道题的关键是要求解以下式子:
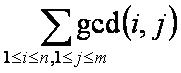
,把它乘以2再减去nm就是最终结果
我们开始对它变形:
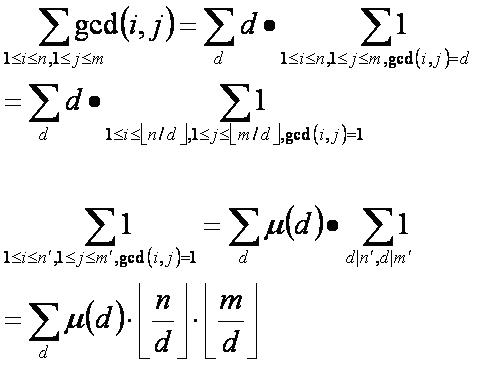
其中
m为莫比乌斯函数,其表达式如下:

这里用它做了一个容斥原理,可以用线性筛法在O(n)时间内求出所有
m的值
接下来如果直接枚举两种d,时间复杂度每次都是O(n),总的为O(n
2)。然而,[n/d]的取值最多只有O(sqrt(n))种,([n/d],[m/d])的取值最多有O(sqrt(n)+sqrt(m))种,所以,可以把每种枚举的时间复杂度降到O(sqrt(n))。总时间复杂度为O(n)。
#include <iostream>
#include <cstdlib>
#include <cstdio>
using namespace std;
int s[100005],prime[40005];
bool b[100005];
void run(int n)
{
int t,i,j,m=0;
s[1]=1;
for(i=2;i<=n;i++)
{
if (!b[i])
{ s[i]=-1; prime[++m]=i; }
for(j=1;(t=i*prime[j])<=n;j++)
{
b[t]=true;
if (i%prime[j]==0)
{ s[t]=0; break; }
s[t]=-s[i];
}
}
}
int n,m;
long long cal(int n,int m)
{
long long res=0;
int i,j1,j2,j;
for(i=1;i<=n&&i<=m;)
{
j1=n/(n/i); j2=m/(m/i);
if (j1<j2) j=j1; else j=j2;
res+=(long long)(s[j]-s[i-1])*(n/i)*(m/i);
i=j+1;
}
return res;
}
int main(void)
{
int t,i,j1,j2,j;
long long res=0;
scanf("%d%d",&n,&m);
if (n<m) { t=n; n=m; m=t; }
run(m); s[0]=0;
for(i=1;i<=n;i++)
s[i]+=s[i-1];
for(i=1;i<=n&&i<=m;)
{
j1=n/(n/i); j2=m/(m/i);
if (j1<j2) j=j1; else j=j2;
res+=(cal(n/i,m/i)*(i+j)*(j-i+1));
i=j+1;
}
printf("%I64d\n",res-(long long)(n)*m);
return 0;
}
posted on 2010-10-13 14:55
zxb 阅读(479)
评论(0) 编辑 收藏 引用