最开始写费用流的时候,有且只会SPFA版的费用流,而且一直都够用,一般来说只要建出了图就赢了,网络流怎么都不会超时。
。。。。这个情况到今天被终结了。。。
终结者见下:
--------------------------------------------------------------------------------------------------------
最优图像
【题目描述】
小E在好友小W的家中发现一幅神奇的图画,对此颇有兴趣。它可以被看做一个包含N×M个像素的黑白图像,为了方便起见,我们用0表示白色像素,1表示黑色像素。小E认为这幅图画暗藏玄机,因此他记录下了这幅图像中每行、每列的黑色像素数量,以回去慢慢研究其中的奥妙。
有一天,小W不慎将图画打湿,原本的图像已经很难分辨。他十分着急,于是找来小E,希望共同还原这幅图画。根据打湿后的图画,他们无法确定真正的图像,然而可以推测出每个像素原本是黑色像素的概率Pij%。那么,一个完整的图像的出现概率就可以定义为 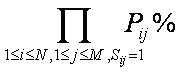 ,其中Sij表示在还原后的图像中,像素是白色(0)还是黑色(1)。换句话说,一个完整图像出现概率就等于其所有黑色像素的出现概率之积。显然,图像的黑色像素不能包含概率为0的像素。
,其中Sij表示在还原后的图像中,像素是白色(0)还是黑色(1)。换句话说,一个完整图像出现概率就等于其所有黑色像素的出现概率之积。显然,图像的黑色像素不能包含概率为0的像素。
然而,小E对此也无能为力。因此他们找到了会编程的小F,也就是你,请你根据以上信息,告诉他们最有可能是原始图像的答案是什么。
【输入文件】
输入文件image.in的第一行是两个正整数N和M,表示图像大小。
接下来N行每行包含M个整数,表示每个像素是黑色像素的概率为Pij%。0 ≤ Pij < 100。
接下来一行有N个非负整数,表示每一行中黑色像素的个数。
接下来一行有M个非负整数,表示每一列中黑色像素的个数。
【输出文件】
输出文件image.out包含一个N×M的01矩阵,表示你还原出的图像。输出不包含空格。图像每行、每列中1的个数必须与输入一致,且是所有可能的图像中出现概率最大的一个。输入数据保证至少存在一个可能的图像。如果有多种最优图像,任意输出一种即可。
【样例输入】
2 2
90 10
20 80
1 1
1 1
【样例输出】
10
01
【样例解释】
共有两种可能的图像:
01
10
和
10
01
前者的出现概率是0.1×0.2=0.02,后者的出现概率是0.9×0.8=0.72,故后者是最优图像。
【数据规模和约定】
对于20%的数据,N , M ≤ 5;
对于100%的数据,N , M ≤ 100。
--------------------------------------------------------------------------------------------------------
这道题的时限是两秒。
这道题的做法是把行和列拿出来,如果i行j列出现1的就把i行与j列连一条流量为1,费用为log(p[i][j])的边。源与每行、每列与汇都连一条流量为行、列1的个数,费用为0的边,然后求最大费用最大流。流过的边所连的行和列的交点就有一个点。
当时看到n<=100,总点数就是2n,心想很小。。。但没想到边有10000条,用SPFA写出来了过后开始只有60分。。后来优化到了70分,就是SPFA极限了,剩下的点根本进不了2秒。
SPFA的时间复杂度是O(km)的,m是边数,k是常数,在这题特殊的图里面一次只能增广1的流量。。所以总的时间复杂度达到了O(100*100*O(SPFA)) > 100000000。。。
于是没办法,把zkw的网络流学了。。
其实zkw网络流增广的时候是sap,修改标号的时候是KM。。。。所以学起来很顺畅,写起来也比SPFA的短,但是效率要高很多:
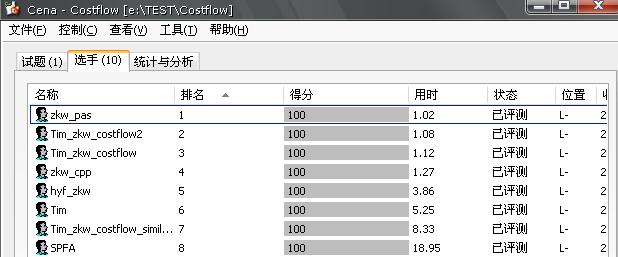
膜拜啊!
代码:
1
 /**//*
/**//*
2 * $File: costflow.cpp
* $File: costflow.cpp
3 */
*/
4
5 #include <iostream>
#include <iostream>
6 #define MAXNODE 500
#define MAXNODE 500
7 #define MAXEDGE MAXNODE*MAXNODE
#define MAXEDGE MAXNODE*MAXNODE
8 #define MIN(a,b) ((a)<(b)?(a):(b))
#define MIN(a,b) ((a)<(b)?(a):(b))
9 #define OPPOSITE(x) (((x)&1)?((x)+1):((x)-1))
#define OPPOSITE(x) (((x)&1)?((x)+1):((x)-1))
10 #define INFINIT ~0U>>1
11
12 using namespace std;
using namespace std;
13
14
15 int n,m;
int n,m;
16 int N,S,T;
int N,S,T;
17 int begin[MAXNODE+1],end[MAXEDGE+1],next[MAXEDGE+1],c[MAXEDGE+1],cost[MAXEDGE+1],d[MAXNODE+1],cur[MAXNODE+1];
int begin[MAXNODE+1],end[MAXEDGE+1],next[MAXEDGE+1],c[MAXEDGE+1],cost[MAXEDGE+1],d[MAXNODE+1],cur[MAXNODE+1];
18 bool hash[MAXNODE+1];
bool hash[MAXNODE+1];
19 int Count = 0;
int Count = 0;
20
 int aug(int u,int f)
int aug(int u,int f) {
{
21 if (u == T) return f;
if (u == T) return f;
22 hash[u] = true;
hash[u] = true;
23 for (int now = cur[u]; now; now = next[now])
for (int now = cur[u]; now; now = next[now])
24 if (c[now]&&!hash[end[now]]&&d[u] == d[end[now]]+cost[now])
if (c[now]&&!hash[end[now]]&&d[u] == d[end[now]]+cost[now])
25 if (int tmp = aug(end[now],MIN(f,c[now])))
if (int tmp = aug(end[now],MIN(f,c[now])))
26 return c[now] -= tmp,c[OPPOSITE(now)] += tmp,cur[u] = now,tmp;
return c[now] -= tmp,c[OPPOSITE(now)] += tmp,cur[u] = now,tmp;
27 return 0;
return 0;
28 }
}
29
 bool modlabel()
bool modlabel() {
{
30 int tmp = INFINIT;
int tmp = INFINIT;
31 for (int i = 1; i<=N; i++)
for (int i = 1; i<=N; i++)
32 if (hash[i])
if (hash[i])
33 for (int now = begin[i]; now; now = next[now])
for (int now = begin[i]; now; now = next[now])
34 if (c[now]&&!hash[end[now]])
if (c[now]&&!hash[end[now]])
35 tmp = MIN(tmp,d[end[now]]+cost[now]-d[i]);
tmp = MIN(tmp,d[end[now]]+cost[now]-d[i]);
36 if (tmp == INFINIT)
if (tmp == INFINIT)
37 return true;
return true;
38 for (int i = 1; i<=N; i++)
for (int i = 1; i<=N; i++)
39 if (hash[i])
if (hash[i])
40 hash[i] = false,d[i] += tmp;
hash[i] = false,d[i] += tmp;
41 return false;
return false;
42 }
}
43
 int CostFlow()
int CostFlow() {
{
44 int costflow = 0,tmp;
int costflow = 0,tmp;
45
 while (true)
while (true) {
{
46 for (int i = 1; i<=N; i++)
for (int i = 1; i<=N; i++)
47 cur[i] = begin[i];
cur[i] = begin[i];
48
 while (tmp = aug(S,~0U>>1))
while (tmp = aug(S,~0U>>1)) {
{
49 costflow += tmp*d[S];
costflow += tmp*d[S];
50 memset(hash,0,sizeof(hash));
memset(hash,0,sizeof(hash));
51 }
}
52 if (modlabel())
if (modlabel())
53 break;
break;
54 }
}
55 return costflow;
return costflow;
56 }
}
57
 void AddEdge(int a,int b,int flow, int v)
void AddEdge(int a,int b,int flow, int v) {
{
58 Count++; next[Count] = begin[a]; begin[a] = Count; end[Count] = b; c[Count] = flow; cost[Count] = v;
Count++; next[Count] = begin[a]; begin[a] = Count; end[Count] = b; c[Count] = flow; cost[Count] = v;
59 Count++; next[Count] = begin[b]; begin[b] = Count; end[Count] = a; c[Count] = 0; cost[Count] = -v;
Count++; next[Count] = begin[b]; begin[b] = Count; end[Count] = a; c[Count] = 0; cost[Count] = -v;
60 }
}
61
 int main()
int main() {
{
62 freopen("costflow.in","r",stdin);
freopen("costflow.in","r",stdin);
63 freopen("costflow.out","w",stdout);
freopen("costflow.out","w",stdout);
64 scanf("%d%d",&n,&m);
scanf("%d%d",&n,&m);
65
 while (m--)
while (m--) {
{
66 int t1,t2,t3,t4;
int t1,t2,t3,t4;
67 scanf("%d%d%d%d",&t1,&t2,&t3,&t4);
scanf("%d%d%d%d",&t1,&t2,&t3,&t4);
68 AddEdge(t1,t2,t3,t4);
AddEdge(t1,t2,t3,t4);
69 }
}
70 S = 1,T = N = n;
S = 1,T = N = n;
71 printf("%d\n",CostFlow());
printf("%d\n",CostFlow());
72 return 0;
return 0;
73 }
}
74
75
今天先休息一下,整理一下思路有时间再详细写下过程~