货币兑换
问题描述
小 Y 最近在一家金券交易所工作。该金券交易所只发行交易两种金券:A 纪
念券(以下简称 A 券)和 B 纪念券(以下简称 B 券)。每个持有金券的顾客都有
一个自己的帐户。金券的数目可以是一个实数。
每天随着市场的起伏波动,两种金券都有自己当时的价值,即每一单位金券
当天可以兑换的人民币数目。我们记录第 K 天中 A 券和 B 券的价值分别为 AK 和
BK (元/单位金券)。
为了方便顾客,金券交易所提供了一种非常方便的交易方式:比例交易法。
比例交易法分为两个方面:
a) 卖出金券:顾客提供一个[0,100]内的实数OP作为卖出比例,其意
义为:将OP%的A券和OP%的B券以当时的价值兑换为人民币;
b) 买入金券:顾客支付IP元人民币,交易所将会兑换给用户总价值为
IP的金券,并且,满足提供给顾客的A券和B券的比例在第K天恰好为RateK;
例如,假定接下来3天内的Ak 、Bk、Ratek 的变化分别为:
时间 Ak Bk Ratek
第一天 1 1 1
第二天 1 2 2
第三天 2 2 3
假定在第一天时,用户手中有100元人民币但是没有任何金券。
用户可以执行以下的操作:
时间 用户操作 人民币(元) A券的数量 B券的数量
开户 无 100 0 0
第一天 买入100元 0 50 50
第二天 卖出50% 75 25 25
第二天 买入60元 15 55 40
第三天 卖出100% 205 0 0
注意到,同一天内可以进行多次操作。
小 Y 是一个很有经济头脑的员工,通过较长时间的运作和行情测算,他已经
知道了未来 N 天内的 A 券和 B 券的价值以及 Rate。他还希望能够计算出来,如
果开始时拥有S元钱,那么N天后最多能够获得多少元钱。
输入文件
第一行两个正整数N、S,分别表示小Y能预知的天数以及初始时拥有的钱数。
接下来N行,第K行三个实数Ak、Bk、Ratek,意义如题目中所述。
输出文件
只有一个实数 MaxProfit,表示第 N 天的操作结束时能够获得的最大的金钱
数目。答案保留3位小数。
输入样例
3 100
1 1 1
1 2 2
2 2 3
输出样例
225.000
样例说明
时间 用户操作 人民币(元) A券的数量 B券的数量
开户 无 100 0 0
第一天 买入100元 0 50 50
第二天 卖出100% 150 0 0
第二天 买入150元 0 75 37.5
第三天 卖出100% 225 0 0
评分方法
本题没有部分分,你的程序的输出只有和标准答案相差不超过0.001时,才能
获得该测试点的满分,否则不得分。
数据规模和约定
测试数据设计使得精度误差不会超过1e-7。
对于40%的测试数据,满足N ≤ 10;
对于60%的测试数据,满足N ≤ 1 000;
对于100%的测试数据,满足N ≤ 100 000;
对于100%的测试数据,满足:
0 < Ak ≤ 10
0 < Bk≤ 10
0 < Ratek ≤ 100
MaxProfit ≤ 1e9
提示
输入文件可能很大,请采用快速的读入方式。
必然存在一种最优的买卖方案满足:
每次买进操作使用完所有的人民币;
每次卖出操作卖出所有的金券。
===================================================================
首先有一个简单的动态规划:
f[i]代表第i天所能得到的最大价值,则:
f[i] = max{f[i - 1], value(j, i) = (在第j天买光f[j]的钱,在第i天卖完所得的价值)}
在第j天卖光可以得到股票B的数量 nb = f[j] / (A[j] * Rate[j] + B[j])
在第j天卖光可以得到股票A的数量 na = nb * Rate[j]
所以value(j, i) = na * A[i] + nb * B[i];
复杂度O(n^2),60分。代码长度 < 1kb
===================================================================
但为了拿后面的40分,就变的很复杂了。。代码长度到了7~8kb。。。
把na和nb看做平面坐标系上的点 X[j], Y[j]
设 P[j] = X[j] * A[i] + Y[j] * B[i]
移项有 Y[j] = (-A[i]/B[i]) X[j] + (P[j] / B[i])
所以当P[j]达到最大的时候,也就是上面的这个一次函数截距最大的时候。
观察可以发现,可以成为最大值的点一定是所有点在一象限以x递增,y递减的一些点构成的凸壳
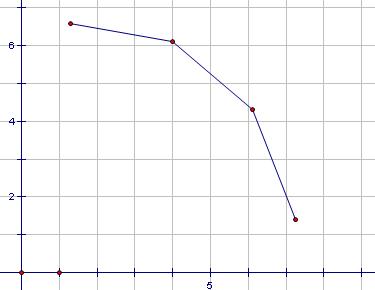
取得最大时:

所以我们要维护这个凸壳上的点。
插入时的维护:
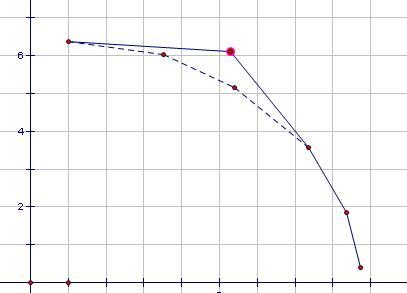
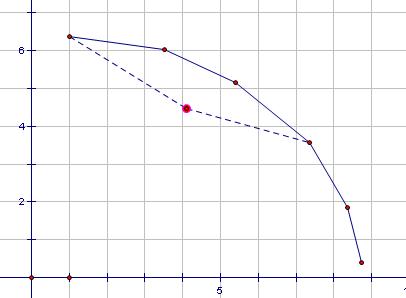
对一条斜率已知的直线查询时:
因为凸壳上斜率递减,所以可以通过对某个点与左右的点所构成直线的斜率进行判断:
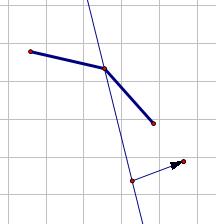
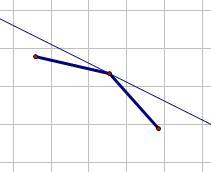
具体维护的时候为了达到较好的复杂度,要用平衡树维护。我选择了Splay,因为有些操作在Splay上面要方便些。。
#include <cstdio>
#include <cstring>
#include <cstdlib>
#include <algorithm>
#include <cmath>
#define MAXN 100000
#define MIN(a,b) ((a) < (b) ? (a) : (b))
#define MAX(a,b) ((a) > (b) ? (a) : (b))
#define INFINITE 1e10
#define EPS 1e-8
using namespace std;
int n;
double f[MAXN + 1];
double A[MAXN + 1], B[MAXN + 1], Rate[MAXN + 1];
double X[MAXN + 1], Y[MAXN + 1];
void Init()
{
scanf("%d%lf", &n, &f[1]);
for (int i = 1; i <= n; i ++)
scanf("%lf%lf%lf", &A[i], &B[i], &Rate[i]);
}
class SplayNode
{
public:
int lt, rt, fa;
double x, y;
};
SplayNode node[MAXN + 1];
int cntNode = 0;
double CrossProduct(double x0, double y0, double x1, double y1, double x2, double y2)
{
return (x1 - x0) * (y2 - y0) - (y1 - y0) * (x2 - x0);
}
double CrossProduct(int a, int b, int c)
{
return CrossProduct(node[a].x, node[a].y,
node[b].x, node[b].y,
node[c].x, node[c].y);
}
class SplayTree
{
private:
int root;
void RightRotate(int x)
{
int lc = node[x].lt, fa = node[x].fa;
node[x].lt = node[lc].rt; node[node[x].lt].fa = x;
node[lc].rt = x, node[x].fa = lc;
if (fa)
{
if (x == node[fa].lt)
node[fa].lt = lc;
else
node[fa].rt = lc;
}
node[lc].fa = fa;
}
void LeftRotate(int x)
{
int rc = node[x].rt, fa = node[x].fa;
node[x].rt = node[rc].lt; node[node[x].rt].fa = x;
node[rc].lt = x, node[x].fa = rc;
if (fa)
{
if (x == node[fa].lt)
node[fa].lt = rc;
else
node[fa].rt = rc;
}
node[rc].fa = fa;
}
void Splay(int x, int FA)
{
int fa, Fa;
while (node[x].fa != FA)
{
fa = node[x].fa;
Fa = node[fa].fa;
if (Fa == FA)
{
if (x == node[fa].lt)
RightRotate(fa);
else
LeftRotate(fa);
}
else
{
if (x == node[fa].lt)
{
if (fa == node[Fa].lt)
{
RightRotate(Fa);
RightRotate(fa);
}
else
{
RightRotate(fa);
LeftRotate(Fa);
}
}
else
{
if (fa == node[Fa].rt)
{
LeftRotate(Fa);
LeftRotate(fa);
}
else
{
LeftRotate(fa);
RightRotate(Fa);
}
}
}
}
if (FA == 0)
root = x;
}
int Pred(int x)
{
if (node[x].lt)
{
x = node[x].lt;
while (true)
{
if (!node[x].rt)
return x;
x = node[x].rt;
}
}
else
{
while (true)
{
if (node[x].fa)
{
if (x == node[node[x].fa].rt)
return node[x].fa;
x = node[x].fa;
}
else
{
return 0;
}
}
}
}
int Succ(int x)
{
if (node[x].rt)
{
x = node[x].rt;
while (true)
{
if (!node[x].lt)
return x;
x = node[x].lt;
}
}
else
{
while (true)
{
if (node[x].fa)
{
if (x == node[node[x].fa].lt)
return node[x].fa;
x = node[x].fa;
}
else
{
return 0;
}
}
}
}
void Del(int now)
{
Splay(now, 0);
int pred = Pred(now), succ = Succ(now);
if (pred && succ)
{
Splay(pred, 0);
Splay(succ, root);
node[node[root].rt].lt = 0;
}
else if (pred && !succ)
{
Splay(pred, 0);
node[root].rt = 0;
}
else if (succ && !pred)
{
Splay(succ, 0);
node[root].lt = 0;
}
else
root = 0;
}
void AdjustLeft(int now)
{
while (true)
{
int p1 = Pred(now), p2 = Pred(p1);
if (p1 && p2)
{
if (CrossProduct(p2, p1, now) >= 0 || node[p1].y <= node[now].y)
Del(p1);
else
break;
}
else if (p1 && node[p1].y <= node[now].y)
{
Del(p1);
}
else
break;
}
}
void AdjustRight(int now)
{
while (true)
{
int p1 = Succ(now), p2 = Succ(p1);
if (p1 && p2)
{
if (CrossProduct(now, p1, p2) >= 0)
Del(p1);
else
break;
}
else
break;
}
}
void Adjust(int now)
{
int pred = Pred(now), succ = Succ(now);
if (pred && succ && CrossProduct(pred, now, succ) >= 0)
Del(now);
else if (succ && node[succ].y >= node[now].y)
Del(now);
else
{
AdjustLeft(now);
AdjustRight(now);
}
}
public:
SplayTree():root(0){}
void Add(double x, double y)
{
int now = root, fa = 0, flag = 0;
while (true)
{
if (!now)
{
now = ++cntNode;
node[now].x = x, node[now].y = y;
node[now].fa = fa;
if (flag == 0)
node[fa].lt = now;
else
node[fa].rt = now;
Splay(now, 0);
break;
}
else
{
fa = now;
if (x <= node[now].x) now = node[now].lt, flag = 0;
else now = node[now].rt, flag = 1;
}
}
Adjust(root);
}
double Calculate(double x, double y, double A, double factor)
{
// y = -(A / factor)x + P / factor
// P = y * factor + A * x
return A * x + y *factor;
}
double Slope(double x, double y)
{
if (fabs(x) < EPS)
return INFINITE;
return y / x;
}
double Ask(double A, double factor)
{
double k = -A / factor;
int now = root, lc, rt;
double x, y;
while (true)
{
double x = node[now].x, y = node[now].y;
int pred = Pred(now), succ = Succ(now);
if (!pred && !succ)
return Calculate(x, y, A, factor);
else if (pred && !succ)
{
if (k <= Slope(x - node[pred].x, y - node[pred].y))
return Calculate(x, y, A, factor);
else
{
if (node[now].lt)
now = node[now].lt;
else
return Calculate(x, y, A, factor);
}
}
else if (!pred && succ)
{
if (k >= Slope(node[succ].x - x, node[succ].y - y))
return Calculate(x, y, A, factor);
else
{
if (node[now].rt)
now = node[now].rt;
else
return Calculate(x, y, A, factor);
}
}
else
{
double kl = Slope(x - node[pred].x, y - node[pred].y);
double kr = Slope(node[succ].x - x, node[succ].y - y);
if (kl >= k && k >= kr)
return Calculate(x, y, A, factor);
else if (k <= kr)
now = node[now].rt;
else
now = node[now].lt;
}
}
}
};
SplayTree T;
int s[MAXN + 1];
void Solve()
{
double minx = INFINITE, maxx = -INFINITE;
/*
* P = X[j] * A[i] + Y[j] * B[i]
* Y[j] = (-A[i] / B[i]) X[j] + P / B[i];
*/
Y[1] = f[1] / (A[1] * Rate[1] + B[1]);
X[1] = Y[1] * Rate[1];
T.Add(X[1], Y[1]);
for (int j = 2; j <= n; j ++)
{
f[j] = f[j - 1];
double v = T.Ask(A[j], B[j]);
f[j] = max(f[j], v);
Y[j] = f[j] / (A[j] * Rate[j] + B[j]);
X[j] = Y[j] * Rate[j];
T.Add(X[j], Y[j]);
}
printf("%.3lf\n", f[n]);
}
int main()
{
freopen("cash.in", "r", stdin);
freopen("cash.out", "w", stdout);
Init();
Solve();
return 0;
}