以下记录，有个人见解，如若有错误，欢迎提出，我一定改正。
附件 ： /Files/MemoryGarden/xuemao.rar
经过了一段时间，终于学会了线段树的基本应用了
线段树的应用非常灵活，我只是学会了皮毛，个人倾向于静态，所以需要以下全局变量。
int tree[max], leftchild[max], rightchild[max], leftvalue[max], rightvalue[max], cover[max],node, coverlength;：
[1] 建树 ：
void construct(int left, int right)
{
int index, mid;
node++;
index = node;
leftvalue[index] = left;
rightvalue[index] = right;
cover[index] = 0;
if(left + 1 < right){
mid = (left + right) / 2;
leftchild[index] = node + 1;
construct(left, mid);
rightchild[index] = node + 1;
construct(mid, right);
}
}上述代码利用二分的方法，建立一棵叶子节点为 (i， i+ 1)的线段树 。 特点是每棵树的根，一定包含于子树的线段。
[2] 插入一段线段：
void insert(int index, int c, int d){
int mid;
if(c <= leftvalue[index] && rightvalue[index] <= d)cover[index]++;
else{
if(leftvalue[index] + 1 < rightvalue[index]){
mid = (leftvalue[index] + rightvalue[index]) / 2;
if(c < mid)insert(leftchild[index], c, d);
if(d > mid)insert(rightchild[index], c, d);
}
}
}
解释 ：当要插入的线段[c, d] 覆盖了线段树上的某段线段的时候，将其标记覆盖的cover[]数组自加。如果不覆盖该线段，分为三种情况，可自己画 一下，再根据当前线段于要插入线段的关系，分情况递归左右子树
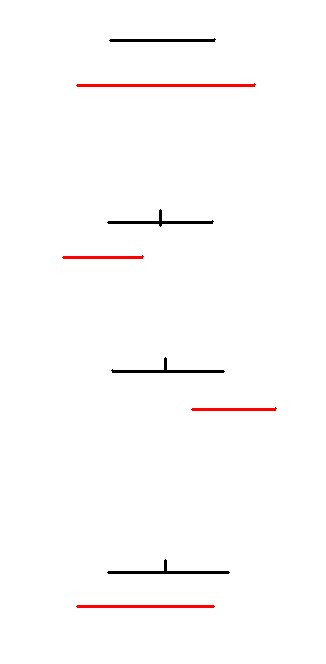
上图1 为覆盖的情况, 运行
if(c <= leftvalue[index] && rightvalue[index] <= d)cover[index]++;
上图2 为 c < mid && d < mid 运行
if(c < mid)insert(leftchild[index], c, d);
上图3 为 c > mid && d > mid 运行
if(d > mid)insert(rightchild[index], c, d);
上图4 为 c < mid && d > mid 运行
if(c < mid)insert(leftchild[index], c, d);
if(d > mid)insert(rightchild[index], c, d);
[3]删除一段线段：
void Delete(int index, int c, int d){
int mid;
if(c <= leftvalue[index] && rightvalue[index] <= d && cover[index])
cover[index]--;
else{
if(leftvalue[index] + 1 < rightvalue[index]){
mid = (leftvalue[index] + rightvalue[index]) / 2;
if(c < mid)Delete(leftchild[index], c, d);
if(d > mid)Delete(rightchild[index], c, d);
}
}
}
与插入一样理解。
[4] 统计：
关于统计，有很多，也很灵活，对于每个题目来说，线段树内每个节点内的要表示的有很多，很灵活，这里只说说测度，也就是最后被覆盖的线段的总长度
void count(int index){
if(cover[index] > 0)total += y[rightvalue[index]] - y[leftvalue[index]];
else{
if(leftvalue[index] + 1 < rightvalue[index]){
count(leftchild[index]);
count(rightchild[index]);
}
}
}
理解 ：既然某段线段的cover[] 是正数，那么，它的子树也一定被cover，因为前面说过的“特点是每棵树的根，一定包含于子树的线段”
所以长度 = 右边界 - 左边界；
以上为线段树的最基本的操作，是对长度的操作。
对于线段树的应用，还有一种比较广泛，就是类似于涂色的问题 ：
很多大大们都介绍过了， 薛茅的论文上讲解的也非常明白
这类问题，大多会有一个bj[]；数组；
这个数组的用处，是当要插入的线段覆盖了线段树的某一节点段时候，拿染色举例，那么以当前节点位根的子树，都会有相同的颜色，所以我们对它的左右儿子做上标记，在每次对线段树上的节点操作的时候，先检查节点的bj[]数组是否被标记过，如若标记过，那么以当前节点为根的子树的颜色都应该是一样的，也就是bj的颜色，然后把当前节点的bj清楚，当前节点的两个儿子设上标记。 说的笨了些，可以参考我上传得pdf && ppt;
对于染色类型的线段树的操作 ：
需要以下的全局变量 只增加了一个bj[]
int tree[max], leftchild[max], rightchild[max], leftvalue[max], rightvalue[max], color[max], bj[max];
int node = 0;
[1] 树的建立 ：
void construct(int left, int right){
int mid, index;
node++;index = node;
leftvalue[index] = left;
rightvalue[index] = right;
color[index] = -2;
bj[index] = -1; //代表未设过标记
if(left + 1 < right){
mid = (left + right) / 2;
leftchild[index] = node + 1;
construct(left, mid);
rightchild[index] = node + 1;
construct(mid, right);
}
}
[2] 处理 bj 节点的clear函数
void clear(int index){
color[index] = bj[index];
bj[leftchild[index]] = bj[index];
bj[rightchild[index]] = bj[index];
bj[index] = -1;
}
仅以颜色举例
[3]树的插入 ：
void insert(int index, int c, int d, int x){
int mid;
if(bj[index] != -1)clear(index);
if(color[index] == x)return;
if(c <= leftvalue[index] && rightvalue[index] <= d)
bj[index] = x;
else{
if(leftvalue[index] + 1 < rightvalue[index]){
color[index] = -1;
mid = (leftvalue[index] + rightvalue[index]) / 2;
if(c < mid)insert(leftchild[index], c, d, x);
if(d > mid)insert(rightchild[index], c, d, x);
}
}
}
解释 ：如果此节点被标记，则当前节点的bj删除，然后两个子节点设上bj
[4] 删除类似
举例 ：
Count the Colors按照上述所说，操作即可 代码如下 ：
#include <stdio.h>
#include <string.h>
#define max 16000
int tree[max], leftchild[max], rightchild[max], leftvalue[max], rightvalue[max], color[max], bj[max];
int node = 0, temp, res[max];
void clear(int index){
color[index] = bj[index];
bj[leftchild[index]] = bj[index];
bj[rightchild[index]] = bj[index];
bj[index] = -1;
}
void construct(int left, int right){
int mid, index;
node++;index = node;
leftvalue[index] = left;
rightvalue[index] = right;
color[index] = -2;
bj[index] = -1; //代表未设过标记
if(left + 1 < right){
mid = (left + right) / 2;
leftchild[index] = node + 1;
construct(left, mid);
rightchild[index] = node + 1;
construct(mid, right);
}
}
void insert(int index, int c, int d, int x){
int mid;
if(bj[index] != -1)clear(index);
if(color[index] == x)return;
if(c <= leftvalue[index] && rightvalue[index] <= d)
bj[index] = x;
else{
if(leftvalue[index] + 1 < rightvalue[index]){
color[index] = -1;
mid = (leftvalue[index] + rightvalue[index]) / 2;
if(c < mid)insert(leftchild[index], c, d, x);
if(d > mid)insert(rightchild[index], c, d, x);
}
}
}
void search(int index){
//printf("search %d \n", index);
if(bj[index] != -1)clear(index);
if(color[index] != -1){
if(color[index] != temp){
if(color[index] >= 0)
res[color[index]]++;
temp = color[index];
}
}else{
search(leftchild[index]);
search(rightchild[index]);
}
}
int main(){
freopen("(a,a+1)segement-color.in", "r", stdin);
freopen("(a,a+1)segement-color.out", "w", stdout);
int i, n, c, d, x;
while(scanf("%d", &n) != -1){
node = 0;
memset(res, 0, sizeof(res));
memset(leftchild, 0, sizeof(leftchild));
memset(rightchild, 0, sizeof(leftchild));
construct(0, 6);
for(i = 0; i < n; i++){
scanf("%d%d%d", &c, &d, &x);
insert(1, c, d, x);
}
search(1);
for(i = 0; i < 8001; i++){
if(res[i])
printf("%d %d\n", i, res[i]);
}
puts("");
}
return 0;
}
关于计算面积的线段树的应用 + 离散化对于离散化，我的理解也不是很清楚 ，不知道理解的对不对。
如果题目的范围很大，而有效的数据又很少，我们可以将有效数据排序，重新建立坐标轴，然后以有效数据的个数作为范围；
比如有整数类型点 4 5 6 7 则 离散后的数组为 f[0] = 4 f[1] = 5 f[2] = 6 f[3] = 7;
或者浮点类型 4.5 5.6 6.54 7.59 离散后的数组为 f[0] = 4.5 f[1] = 5.6 f[2] = 6.54 f[3] = 7.59;
这样我们就把浮点类型，或者整数类型的有效数据转映射到正数下标的数组里面去了。
我们可以建立一棵(0, 4)的线段树 当插入一条线段 [0， 1] 代表我们插入了[4---5] 或者 [4.5---5.6] 这样一条线段，由于我们将有效数据排序，所以f数组的下表与有效数据的同为递增的关系，所以当我们插入[0， 3]这条线段的时候，也代表了我们插入了[4---7] 或者[4.5---7.59]这样一条线段，[0， 3] 覆盖了[0， 1]这条线段，同样，[4---7] 也会覆盖 [4---5] 或者[4.5---7.59] 也会覆盖[4.5---5.6] 。
以上就是我对离散化的理解了。
举例一题 ：
Atlantis 这个题目我们就把横纵坐标都进行离散，然后对于纵坐标，用线段树操作。
把竖直的线段离散后，存储在一个结构体中，存储x坐标, 和上下两端的y坐标，kind用于标记对于一个矩形来说，左边的竖线，还是右边竖线
struct L{
double x, y1, y2;
bool kind;
}line[max];
把纵坐标离散，然后排序。按照我上面离散化的意思，建树。
我用的是<map> 能标记重复，也能排序
map<double, int> Y;
map<double, int>::iterator it;
对line 数组按照x坐标排序，对于line数组，逐2个计算横坐标的差，总坐标若为左竖线，则插入，若为右竖线，则删除。。。。说得太不明白了，连我自己都不明白。还是看看代码吧 请大家自己理解。
代码写的不好，在poj上不是0ms。
#include <stdio.h>
#include <string.h>
#include <algorithm>
#include <map>
#include <math.h>
#define max 401
#define eps 1e-8
using namespace std;
int tree[max], leftchild[max], rightchild[max], rightvalue[max], leftvalue[max], cover[max];
int node, linelength;
double y[max * 2], total;
struct L{
double x, y1, y2;
bool kind;
}line[max];
map<double, int> Y;
map<double, int>::iterator it;
bool cmp(L a, L b){
return a.x < b.x;
}
void construct(int left, int right){
int index, mid;
node++;
index = node;
leftvalue[index] = left;
rightvalue[index] = right;
cover[index] = 0;
if(left + 1 < right){
mid = (left + right) / 2;
leftchild[index] = node + 1;
construct(left, mid);
rightchild[index] = node + 1;
construct(mid, right);
}
}
void insert(int index, int c, int d){
int mid;
if(c <= leftvalue[index] && rightvalue[index] <= d)cover[index]++;
else{
if(leftvalue[index] + 1 < rightvalue[index]){
mid = (leftvalue[index] + rightvalue[index]) / 2;
if(c < mid)insert(leftchild[index], c, d);
if(d > mid)insert(rightchild[index], c, d);
}
}
}
void Delete(int index, int c, int d){
int mid;
if(c <= leftvalue[index] && rightvalue[index] <= d && cover[index])
cover[index]--;
else{
if(leftvalue[index] + 1 < rightvalue[index]){
mid = (leftvalue[index] + rightvalue[index]) / 2;
if(c < mid)Delete(leftchild[index], c, d);
if(d > mid)Delete(rightchild[index], c, d);
}
}
}
void count(int index){
if(cover[index] > 0)total += y[rightvalue[index]] - y[leftvalue[index]];
else{
if(leftvalue[index] + 1 < rightvalue[index]){
count(leftchild[index]);
count(rightchild[index]);
}
}
}
int main(){
freopen("1043.in", "r", stdin);
freopen("1043.out", "w", stdout);
int n, i, j, num, c, d, o = 1;
double lx, ly, rx, ry, area;
while(scanf("%d", &n), n){
linelength = node = num = 0;
Y.clear();area = total = 0.0;
for(i = 0; i < n; i++){
scanf("%lf%lf%lf%lf", &lx, &ly, &rx, &ry);
line[linelength].x = lx;
line[linelength].y1 = ly;
line[linelength].kind = true;
line[linelength++].y2 = ry;
line[linelength].x = rx;
line[linelength].y1 = ly;
line[linelength].kind = false;
line[linelength++].y2 = ry;
it = Y.find(ly);
if(it == Y.end())Y.insert(make_pair(ly, num++));
it = Y.find(ry);
if(it == Y.end())Y.insert(make_pair(ry, num++));
}
for(it = Y.begin(), i = 0; it != Y.end(); it++, i++){
y[i] = it->first;
it->second = i;
}
sort(line, line + linelength, cmp);
construct(0, num);
for(i = 0; i < linelength - 1; i++){
c = Y.find(line[i].y1)->second;
d = Y.find(line[i].y2)->second;
if(line[i].kind)insert(1, c, d);
else Delete(1, c, d);
total = 0.0;
count(1);
area += total * (line[i + 1].x - line[i].x);
}
printf("Test case #%d\nTotal explored area: %.2lf\n\n", o++, area);
}
return 0;
}
ps ：切记 如果要建立一棵[0， a] 的一棵线段树，我们需要2 * a 个节点。 我因为这个wa了n次。
这是我所有学过的线段树的知识，还会继续学习，如果有毛病，请大家指出，菜鸟在这里谢过；