均分纸牌。。。以前在做这个题目的时候，老师给了思路：就是从第一项开始加，可以让前i堆平均为止，移动次数就是i-1了！然后继续扫描下去！累加移动次数就是所求解！

按照这种思路，我那时直接写了代码完事了，其实这是很不好的！呵呵。。。虽然我们可以通过参考别人的思路解决问题，但是这我们应该更多的学习，如何从他人的解题思路里获得自己解决类似问题的思路，如何产生思路！！！

    解题代码一（按照老师的思路，我以前写的）

#include<stdio.h>
int main()
{
    int  n,sum,v,sum1;
    int s[100];
    int i,j;
    int count;
     scanf("%d",&n);
    do{
        sum=0;
        sum1=0;
        v=0;
        j=0;
        count=0;
    for(i=0;i<n;i++)
    {
        scanf("%d",&s[i]);
        sum=sum+s[i];
    }

    v=sum/n;

    for(i=0;i<n;i++)
    {
        sum1=sum1+s[i];
        j=j+1;
        if((sum1%v==0)&&(sum1==v*j))
        {
            count=count+j-1;
            sum1=0;
            j=0;            
        }
    }
      printf("%d\n",count);
       scanf("%d",&n);
    }while(n!=0);
}

      今天，我又搜了一下，到底为啥是这么个解题思路，这让我困惑了昨天一个晚上！！更可悲的是，搜出来这个题目尽然是小学生数奥里得题目。。。

      算了还是直切正题，如果有n堆纸牌要均分（当然可以均分成功），我们假设第一堆有纸牌，其他堆都没有，那我们只要从第一推开始移动（总数-平均值）张纸牌，一堆堆往下分就解决了，这多好呀，移动次数肯定是最少的。。

      当然这只是种假设，跟多的时候是，每一堆得纸牌都有几张，这个时候上面这种分法自然不行了，但是上面这种分法给了我们一种最少移动的思路，就是每次都把i堆分好了。。思考一下，但是新的问题又出现，不是每一堆都可以通过后一堆给（或者前一堆要）从而达到平均的，万一后（前）一堆不够了怎么办？

         网上走了一遭，发现纸牌数量还可以为负！一开始我也不理解，牌数为负，就跟人可以半个没啥两样，简直就是自欺欺人！但是我回家想了下，牌数为负，固然是不对的，但是至少他在传达着一种信息，我要牌！！！而且我要的是前i堆牌能够达到平均值的数量，当然我们也知道，n堆纸牌是肯定能够被平分的，就是在说最后肯定有一堆可以满足前i堆的牌！自然他也会给他前一堆请求所需的牌，这就跟我前面举只有第一堆有牌的情况一样了，只是给的时候牌数不同，可见负牌其实传达的是这种意思，而且移动次数为满足i~j堆平分的堆数减一，即移动j-i-1次！！！于是我又写了牌数可负的代码：

解题代码二如下（牌数可负）：

#include<stdio.h>
#include<string.h>
int main()
{
    int  n,sum,v;
    int s[100];
    int i,j;
    while(scanf("%d",&n)!=EOF&&n!=0)
    {
        sum=0;
        v=0;
        j=0;
        for(i=0;i<n;i++)
        {
            scanf("%d",&s[i]);
            sum=sum+s[i];
        }

        v=sum/n;

        for(i=0;i<n-1;i++)
        {
            if(s[i]<v)
            {
                s[i+1]=s[i+1]-(v-s[i]);
                j++;
            }
            else if(s[i]>v)
            {
                s[i+1]=s[i+1]+(s[i]-v);
                j++;
            }
        }
       
        
       printf("%d\n",j);
    }
    return 0;
}

写完后我发现其实每次找到可以满足条件的一堆牌，它都会把前面的所有堆分好！网上说这是贪心算法，但是我觉得这个贪心跟动态规划差不多，可能还要难，因为它在动态规划的基础上，还要分析和总结。首先，他要找最优子结构（这个最有子结构很隐蔽），在这里找到一个找到可以给（发）牌的堆，事实上，这样的也就找到了一个连续x堆可平分的子结构 ！其次，总结最优子结构的性质，最后发现牌数可以为负以及意义，然后发现一堆一堆往下分就是结果！最后就是老师这样算了！！！这个过程其实很复杂。。。

 我觉得这样还不过瘾，我又写了个这种思路下的分牌结果输出程序，其实也可以计算移动次数（不过我觉得没啥必要了！！）

代码如下：

#include<stdio.h>
#include<string.h>
int temp;
void move(int i,int v,int s[100],int d[100])
{
    if(i<0||d[i]==0)    //i<0,不用解释了，d[i]==0代表前i堆都分配好了
        return;
    if(d[i]==1)            //从后一堆拿
    {
        printf("从第%d堆纸牌向%d堆纸牌移动%d张!\n",i+1,i,v-s[i]);
        move(i-1,v,s,d);    //递归
        d[i]=0;                //置零，其实一次递归就可以让前i堆都分配成功！
    }
    
    else if(d[i]==2)    //给后一堆
    {
        printf("从第%d堆纸牌向%d堆纸牌移动%d张!\n",i,i+1,s[i]-v);
        d[i]=0;
    }
}

//处理当前i堆函数。。。其实我自己也不知道怎么定义这个函数才对
/**//*
参数说明：
i：当前堆
v：平均值
s：堆状态序列值
d：记录分配情况：1代表向后一堆取，2代表向后一堆给，0代表本堆已经是平均值了，没有操作
n：堆数
*/
void mypow(int i,int v,int s[100],int d[100],int n)
{
    if(i==n)            //前n-1堆分配成功后，第n堆一定是平均值，所以直接返回
        return;
    if(s[i]<v)            //如果本堆小于平均值，就向前一堆去要
    {
         d[i]=1;
         if(s[i+1]-(v-s[i])>=0)        //如果前一堆可以给，就直接移动,事实上这次给可以让前i堆纸牌值全部为平均值
         {
              temp=1;
              move(i,v,s,d);        //移动函数
         }
        s[i+1]=s[i+1]-(v-s[i]);        //第i+1堆状态变化
        mypow(i+1,v,s,d,n);            //递归求解i+1堆
    }
    else if(s[i]>v)                    //如果本堆大于平均值，就给后一堆
    {
        s[i+1]=s[i+1]+(s[i]-v);
        d[i]=2;
        temp=1;
        move(i,v,s,d);                //这里的move其实可以直接写成printf
        mypow(i+1,v,s,d,n);            //递归求解i+1堆
    }
    else if(s[i]==v)                //如果本堆等于平均值，当然不用移动了
    {
        d[i]=0;
        mypow(i+1,v,s,d,n);            //递归求解i+1堆
    }
    return;
}
int main()
{
    int n,sum,v;
    int s[100],d[100];
    int i;
    int count;
    while(scanf("%d",&n)!=EOF&&n!=0)
    {
        memset(d,0,sizeof(d));
        sum=0;
        v=0;
        count=0;
        for(i=1;i<=n;i++)
        {
            scanf("%d",&s[i]);
            sum=sum+s[i];
        }

        v=sum/n;
        temp=0;
        mypow(1,v,s,d,n);
        if(!temp)                //这个就是不用分配标记
            printf("不用移动了！\n");
    }
    return 0;
}

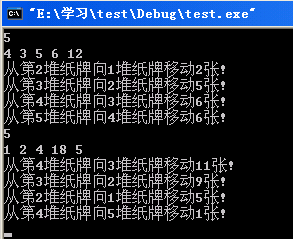
运行结果如下：