有一段输入的离散信号{Zi},假定这段信号长度为N(N=2^n)。
Q1:
通常,可以用Fourier Transform来进行频域分析。例如对于一段随机白噪,可以得出时域和频域的图像如下:
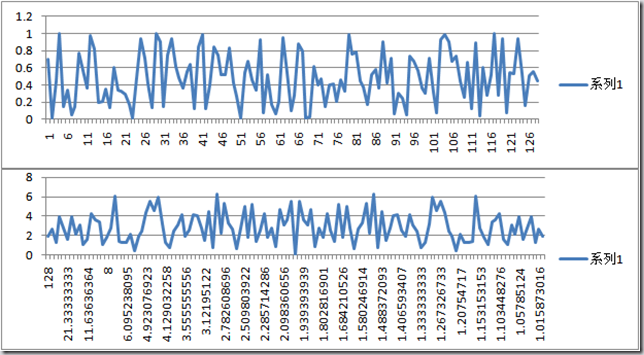
其中,上图为时域,横轴t,纵轴为Zt。下图为频域,横轴为1/f(即周期T),纵轴为|Fn|(波幅)。
如果有这样一种假说,一个信号,是由一个基频与若干高/低频谐波和噪声的混合,且基频、噪声和高/低频谐波的波幅存在着一定的分布率,例如指数分布,例如,假设基频波幅期望是t(0<t<1),而次一级的谐波/噪声波幅的期望为t^2,以此类推。且信号的波幅是随机的,其波幅概率曲线成正态分布。
问题:有没有一种办法,可以对频谱加以分析,判断出可能概率最大的基频频率,并给出这一判断的概率是多少。(要做假设检验用,例如90%)
Q2:
使用一个信号发生器,Zi = 1 + Sin( i * Pi / 20 )。并经过傅里叶分析,得出以下的时域和频域统计:
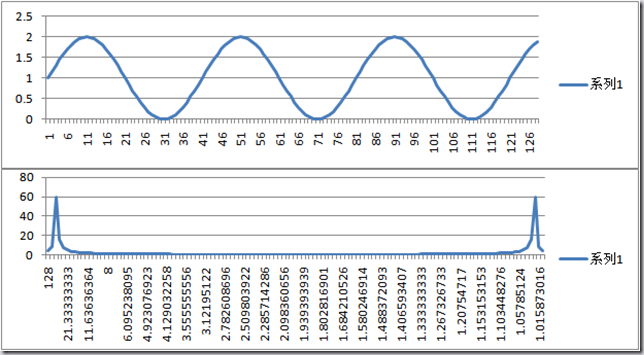
其中,上图为时域,横轴t,纵轴为Zt。下图为频域,横轴为1/f(即周期T),纵轴为|Fn|(波幅)。
问题:为什么在周期接近1的时候,会有一个波幅尖峰?