《算法艺术与信息学竞赛》P-116:
提交方式:POJ1191
好久没有写文章了,随便放一个题目在这里凑数:
题目描述:
棋盘分割
| Time Limit: 1000MS |
|
Memory Limit: 10000K |
| Total Submissions: 1302 |
|
Accepted: 463 |
Description
将一个8*8的棋盘进行如下分割:将原棋盘割下一块矩形棋盘并使剩下部分也是矩形,再将剩下的部分继续如此分割,这样割了(n-1)次后,连同最后剩下的矩形棋盘共有n块矩形棋盘。(每次切割都只能沿着棋盘格子的边进行)
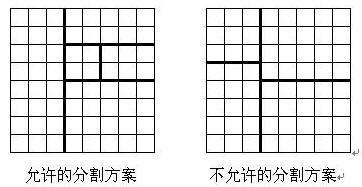
原棋盘上每一格有一个分值,一块矩形棋盘的总分为其所含各格分值之和。现在需要把棋盘按上述规则分割成n块矩形棋盘,并使各矩形棋盘总分的均方差最小。
均方差
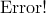
,其中平均值
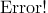
,x
i为第i块矩形棋盘的总分。
请编程对给出的棋盘及n,求出O'的最小值。
Input
第1行为一个整数n(1 < n < 15)。
第2行至第9行每行为8个小于100的非负整数,表示棋盘上相应格子的分值。每行相邻两数之间用一个空格分隔。
Output
仅一个数,为O'(四舍五入精确到小数点后三位)。
Sample Input
3
1 1 1 1 1 1 1 3
1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 0
1 1 1 1 1 1 0 3
Sample Output
1.633
Source
Noi 99
解题思路:
参照《算法艺术与信息学竞赛》:
代码:
1 /*********************************************************************
2 Author: littlekid
3 Created Time: 2008-2-27 17:08:36
4 Problem Source: POJ1191
5 Description:
6 ********************************************************************/
7 # include <iostream>
8 # include <cmath>
9 using namespace std;
10
11 const int maxint = 2000000000;
12
13 # define N 8
14
15 double ans;
16 int map[ N+1 ][ N+1 ], n;
17 int sum[ N+1 ][ N+1 ];//[ N+1 ][ N+1 ];
18 int f[16][ N+1 ][ N+1 ][ N+1 ][ N+1 ];
19
20 void init()
21 {
22 for (int i = 1; i <= N; i ++)
23 {
24 for (int j = 1; j <= N; j++)
25 {
26 scanf("%d", &map[i][j]);
27 }
28 }
29 }
30
31 void output()
32 {
33 printf("%.3lf\n", ans);
34 }
35
36 inline int cal_sum(int x1, int y1, int x2, int y2)
37 {
38 int tmp = sum[x2][y2]+sum[x1-1][y1-1] - sum[x1-1][y2]-sum[x2][y1-1];
39 return tmp*tmp;
40 }
41
42
43 void dp()
44 {
45 //
46 memset(sum, 0, sizeof(sum));
47 int tmp;
48 sum[0][0] = 0;
49 for (int i = 1; i <= N; i ++)
50 {
51 for (int j = 1; j <= N; j ++)
52 {
53 sum[i][j] = sum[i][j-1]+sum[i-1][j] - sum[i-1][j-1] + map[i][j];
54 }
55 }
56 memset(f, 0, sizeof(f));
57 for(int x1 = 1; x1 <= N; x1 ++)
58 {
59 for (int y1 = 1; y1 <= N; y1 ++)
60 {
61 for (int x2 = x1; x2 <= N; x2 ++)
62 {
63 for (int y2 = y1; y2 <= N; y2 ++)
64 {
65 f[1][x1][y1][x2][y2] = cal_sum(x1, y1, x2, y2);
66 }
67 }
68 }
69 }
70 for (int k = 2; k <= n; k ++)
71 {
72
73 for (int x1 = 1; x1 <= N; x1 ++)
74 {
75 for (int y1 = 1; y1 <= N; y1 ++)
76 {
77 for (int x2 = x1; x2 <= N; x2 ++)
78 {
79 for (int y2 = y1; y2 <= N; y2 ++)
80 {
81
82 f[k][x1][y1][x2][y2] = maxint;
83 for (int x = x1; x < x2; x ++)
84 {
85 tmp = min( f[k-1][x1][y1][x][y2] + cal_sum(x+1, y1, x2, y2), //sum[x+1][y1][x2][y2],
86 f[k-1][x+1][y1][x2][y2] + cal_sum(x1, y1, x, y2)); //sum[x1][y1][x][y2] );
87 if (f[k][x1][y1][x2][y2] > tmp) f[k][x1][y1][x2][y2] = tmp;
88 }
89 for (int y = y1; y < y2; y ++)
90 {
91 tmp = min( f[k-1][x1][y1][x2][y] + cal_sum(x1, y+1, x2, y2), //sum[x1][y+1][x2][y2],
92 f[k-1][x1][y+1][x2][y2] + cal_sum(x1, y1, x2, y) ); //sum[x1][y1][x2][y] );
93 if (f[k][x1][y1][x2][y2] > tmp) f[k][x1][y1][x2][y2] = tmp;
94 }
95 }
96 }
97 }
98 }
99 }
100 // cout << f[n][1][1][N][N] << endl; ///
101 ans = sqrt( f[n][1][1][N][N]/(double)n - sum[N][N]*sum[N][N]/(double)(n*n));
102 }
103
104 int main()
105 {
106 while (scanf("%d", &n) != EOF)
107 {
108 init();
109 dp();
110 output();
111 }
112 return 0;
113 }
114
115
posted on 2008-02-27 20:04
R2 阅读(1957)
评论(1) 编辑 收藏 引用 所属分类:
Problem Solving