参考网上他人的经验,写了一个基于邻接表的有向图类,实现了图的基本操作和Dijkstra算法。
适合大数据量的图。
代码如下:
#ifndef __GRAPH_H__
#define __GRAPH_H__
#include <vector>
#define IN
#define OUT
#define INOUT
using namespace std;
namespace graphspace
{
template <typename weight>
struct Edge
{
int nDestVertex;
weight edgeWeight;
Edge<weight> *pNextEdge;
Edge(int d, weight c, Edge<weight> *p = NULL)
:nDestVertex(d), edgeWeight(c), pNextEdge(p)
{}
};
template <typename vertexNametype, typename weight>
struct Vertex
{
vertexNametype vertexName;
Edge<weight> *pAdjEdges;
Vertex(vertexNametype x, Edge<weight> *p = NULL)
:vertexName(x), pAdjEdges(p)
{}
};
//adjacency list based graph
template <typename vertexNametype, typename weight>
class ALGraph
{
public:
explicit ALGraph();
~ALGraph();
public:
bool insertAVertex(IN const vertexNametype vertexName);
bool insertAEdge(IN const vertexNametype vertexName1, IN const vertexNametype vertexName2, IN const weight edgeWeight);
bool removeAEdge(IN const vertexNametype vertexName1, IN const vertexNametype vertexName2, IN const weight edgeWeight);
weight getMinWeight(IN const vertexNametype vertexName1, IN const vertexNametype vertexName2);
int getVertexIndex(IN const vertexNametype vertexName);
int getVertexNumber();
vertexNametype getData(IN int index);
int Dijkstra(IN const vertexNametype vertexName1);
void DijkstraPrint(IN int index, IN int sourceIndex, IN vector<int> vecPreVertex);
friend ostream& operator<<(OUT ostream &out, IN const ALGraph<vertexNametype,weight> &graphInstance);
public:
weight getEdgeWeight(IN const Edge<weight> *pEdge);
void getVertexEdgeWeight(IN const int v1, OUT vector<weight> &DistanceArray);
vector< Vertex<vertexNametype, weight> > m_vertexArray;
};
#include "graph_realize.h"
}
#endif
实现类头文件:
#ifndef __GRAPH_REALIZE__H_
#define __GRAPH_REALIZE__H_
/*#define VERTEXARRAYITE (vector< Vertex<vertexNametype, weight> >::iterator) */
template<typename vertexNametype, typename weight>
ALGraph<vertexNametype, weight>::ALGraph()
{
if (!m_vertexArray.empty())
{
m_vertexArray.clear();
}
}
template<typename vertexNametype, typename weight>
ALGraph<vertexNametype, weight>::~ALGraph()
{
vector< Vertex<vertexNametype, weight> >::iterator iter;
for(iter = m_vertexArray.begin(); iter != m_vertexArray.end(); iter++)
{
Edge<weight> *p = iter->pAdjEdges;
while(NULL != p)
{
iter->pAdjEdges = p->pNextEdge;
delete p;
p = iter->pAdjEdges;
}
}
if (!m_vertexArray.empty())
{
m_vertexArray.clear();
}
}
template<typename vertexNametype, typename weight>
bool ALGraph<vertexNametype, weight>::insertAVertex(IN const vertexNametype vertexName)
{
Vertex<vertexNametype, weight> VertexInstance(vertexName, NULL);
m_vertexArray.push_back(VertexInstance);
return true;
}
template<typename vertexNametype, typename weight>
bool ALGraph<vertexNametype, weight>::insertAEdge(IN const vertexNametype vertexName1,
IN const vertexNametype vertexName2, IN const weight edgeWeight)
{
int v1 = getVertexIndex(vertexName1);
if (-1 == v1)
{
cerr << "There is no vertex 1" << endl;
return false;
}
int v2 = getVertexIndex(vertexName2);
if (-1 == v2)
{
cerr << "There is no vertex 2" << endl;
return false;
}
Edge<weight> *p = m_vertexArray.at(v1).pAdjEdges;
while(p != NULL && p->nDestVertex != v2)
{
p = p->pNextEdge;
}
if (NULL == p)
{
p = new Edge<weight>(v2, edgeWeight, m_vertexArray.at(v1).pAdjEdges);
m_vertexArray.at(v1).pAdjEdges = p;
return true;
}
if (v2 == p->nDestVertex)
{
Edge<weight> *q = p;
p = new Edge<weight>( v2, edgeWeight, q->pNextEdge );
q->pNextEdge = p;
return true;
}
return false;
}
template<typename vertexNametype, typename weight>
bool ALGraph<vertexNametype, weight>::removeAEdge(IN const vertexNametype vertexName1,
IN const vertexNametype vertexName2, IN const weight edgeWeight)
{
int v1 = getVertexIndex(vertexName1);
if (-1 == v1)
{
cerr << "There is no vertex 1" << endl;
return false;
}
int v2 = getVertexIndex(vertexName2);
if (-1 == v2)
{
cerr << "There is no vertex 2" << endl;
return false;
}
Edge<weight> *p = m_vertexArray.at(v1).pAdjEdges;
Edge<weight> *q = NULL;
while(p != NULL && p->nDestVertex != v2 )
{
q = p;
p = p->pNextEdge;
}
if (NULL == p)
{
cerr << "Edge is not found" << endl;
return false;
}
while( edgeWeight != p->edgeWeight && p->nDestVertex == v2)
{
q = p;
p = p->pNextEdge;
}
if (v2 != p->nDestVertex)
{
cerr << "Edge is not found" << endl;
return false;
}
q->pNextEdge = p->pNextEdge;
delete p;
return true;
}
template<typename vertexNametype, typename weight>
weight ALGraph<vertexNametype, weight>::getEdgeWeight(IN const Edge<weight> *pEdge)
{
return pEdge->edgeWeight;
}
template<typename vertexNametype, typename weight>
void ALGraph<vertexNametype, weight>::getVertexEdgeWeight(IN const int v1, OUT vector<weight> &DistanceArray)
{
Edge<weight> *p = m_vertexArray.at(v1).pAdjEdges;
int prevIndex = -1;
weight tmp;
while(NULL != p)
{
//consider the same edges exist
if (prevIndex == p->nDestVertex)
{
if (tmp > p->edgeWeight)
{
DistanceArray[prevIndex] = p->edgeWeight;
}
}
else
{
DistanceArray[p->nDestVertex] = p->edgeWeight;
prevIndex = p->nDestVertex;
tmp = p->edgeWeight;
}
p = p->pNextEdge;
}
}
template<typename vertexNametype, typename weight>
weight ALGraph<vertexNametype, weight>::getMinWeight(IN const vertexNametype vertexName1,
IN const vertexNametype vertexName2)
{
Edge<weight> *pEdge = NULL;
int v1 = getVertexIndex(vertexName1);
if (-1 == v1)
{
cerr << "There is no vertex 1" << endl;
return false;
}
int v2 = getVertexIndex(vertexName2);
if (-1 == v2)
{
cerr << "There is no vertex 2" << endl;
return false;
}
Edge<weight> *p = m_vertexArray.at(v1).pAdjEdges;
while (p != NULL && p->nDestVertex != v2)
{
p = p->pNextEdge;
}
if (NULL == p)
{
pEdge = NULL;
return weight(0);
}
weight tmp = getEdgeWeight(p);
pEdge = p;
while (NULL != p && v2 == p->nDestVertex)
{
if (tmp > getEdgeWeight(p))
{
tmp = getEdgeWeight(p);
pEdge = p;
}
p = p->pNextEdge;
}
return tmp;
}
template<typename vertexNametype, typename weight>
int ALGraph<vertexNametype, weight>::getVertexIndex(IN const vertexNametype vertexName)
{
for (int i = 0; i < m_vertexArray.size(); i++)
{
if (vertexName == getData(i))
{
return i;
}
}
return -1;
}
template<typename vertexNametype, typename weight>
int ALGraph<vertexNametype, weight>::getVertexNumber()
{
return m_vertexArray.size();
}
template<typename vertexNametype, typename weight>
vertexNametype ALGraph<vertexNametype, weight>::getData(IN int index)
{
return m_vertexArray.at(index).vertexName;
}
template<typename vertexNametype, typename weight>
int ALGraph<vertexNametype, weight>::Dijkstra(IN const vertexNametype vertexName1)
{
int sourceIndex = getVertexIndex(vertexName1);
if (-1 == sourceIndex)
{
cerr << "There is no vertex " << endl;
return false;
}
int nVertexNo = getVertexNumber();
//the array to record the points have been included, if included the value is true
//else is false
vector<bool> vecIncludeArray;
vecIncludeArray.assign(nVertexNo, false);
vecIncludeArray[sourceIndex] = true;
//the array to record the distance from vertex1
vector<weight> vecDistanceArray;
vecDistanceArray.assign(nVertexNo, weight(INT_MAX));
vecDistanceArray[sourceIndex] = weight(0);
//prev array to record the previous vertex
vector<int> vecPrevVertex;
vecPrevVertex.assign(nVertexNo, sourceIndex);
getVertexEdgeWeight(sourceIndex, vecDistanceArray);
int vFrom, vTo;
while(1)
{
weight minWeight = weight(INT_MAX);
vFrom = sourceIndex;
vTo = -1;
for (int i = 0; i < nVertexNo; i++)
{
if (!vecIncludeArray[i] && minWeight > vecDistanceArray[i])
{
minWeight = vecDistanceArray[i];
vFrom = i;
}
}
if (weight(INT_MAX) == minWeight)
{
break;
}
vecIncludeArray[vFrom] = true;
Edge<weight> *p = m_vertexArray[vFrom].pAdjEdges;
while (NULL != p)
{
weight wFT = p->edgeWeight;
vTo = p->nDestVertex;
if (!vecIncludeArray[vTo] && vecDistanceArray[vTo] > wFT + vecDistanceArray[vFrom])
{
vecDistanceArray[vTo] = wFT + vecDistanceArray[vFrom];
vecPrevVertex[vTo] = vFrom;
}
p = p->pNextEdge;
}
}
//print the shortest route of all vertexes
for (int i = 0; i < nVertexNo; i++)
{
if (weight(INT_MAX) != vecDistanceArray[i])
{
cout << getData(sourceIndex) << "->" << getData(i) << ": ";
DijkstraPrint(i, sourceIndex, vecPrevVertex);
cout << " " << vecDistanceArray[i];
cout << endl;
}
}
return 0;
}
template<typename vertexNametype, typename weight>
void ALGraph<vertexNametype, weight>::DijkstraPrint(IN int index, IN int sourceIndex, IN vector<int> vecPreVertex)
{
if (sourceIndex != index)
{
DijkstraPrint(vecPreVertex[index], sourceIndex, vecPreVertex);
}
cout << getData(index) << " ";
}
template<typename vertexNametype, typename weight>
ostream& operator<<(OUT ostream &out, IN ALGraph<vertexNametype,weight> &graphInstance)
{
int vertexNo = graphInstance.getVertexNumber();
out << "This graph has " << vertexNo << "vertexes" << endl;
for(int i = 0; i < vertexNo; i++)
{
vertexNametype x1 = graphInstance.getData(i);
out << x1 << ": ";
Edge<weight> *p = graphInstance.m_vertexArray.at(i).pAdjEdges;
while (NULL != p)
{
out << "(" << x1 << "," << graphInstance.getData(p->nDestVertex) << "," << p->edgeWeight << ") ";
p = p->pNextEdge;
}
out << endl;
}
return out;
}
#endif
基本测试:
#include <iostream>
#include "graph.h"
using namespace std;
using namespace graphspace;
void main()
{
ALGraph<char, int> g;
g.insertAVertex( 'A' );
g.insertAVertex( 'B' );
g.insertAVertex( 'C' );
g.insertAVertex( 'D' );
g.insertAVertex('E');
g.insertAVertex('F');
cout << g << endl << endl;
g.insertAEdge('A', 'B', 6);
g.insertAEdge('A', 'C', 3);
g.insertAEdge('B', 'C', 2);
g.insertAEdge('B', 'D', 5);
g.insertAEdge('C', 'D', 3);
g.insertAEdge('C', 'E', 4);
g.insertAEdge('D', 'E', 2);
g.insertAEdge('D', 'F', 3);
g.insertAEdge('E', 'F', 5);
g.insertAEdge('B', 'A', 6);
g.insertAEdge('C', 'A', 3);
g.insertAEdge('C', 'B', 2);
g.insertAEdge('D', 'B', 5);
g.insertAEdge('D', 'C', 3);
g.insertAEdge('E', 'C', 4);
g.insertAEdge('E', 'D', 2);
g.insertAEdge('F', 'D', 3);
g.insertAEdge('F', 'E', 5);
cout << g << endl << endl;
g.Dijkstra('A');
system("pause");
return;
}
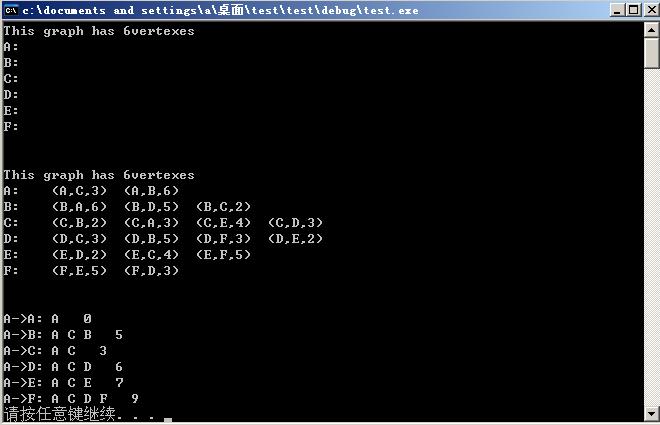
测试结果:
posted on 2010-07-30 14:30
saha 阅读(5480)
评论(1) 编辑 收藏 引用