Accumulation Degree
| Time Limit: 5000MS |
|
Memory Limit: 65536K |
| Total Submissions: 248 |
|
Accepted: 30 |
Description
Trees
are an important component of the natural landscape because of their
prevention of erosion and the provision of a specific ather-sheltered
ecosystem in and under their foliage. Trees have also been found to
play an important role in producing oxygen and reducing carbon dioxide
in the atmosphere, as well as moderating ground temperatures. They are
also significant elements in landscaping and agriculture, both for
their aesthetic appeal and their orchard crops (such as apples). Wood
from trees is a common building material.
Trees also play an
intimate role in many of the world's mythologies. Many scholars are
interested in finding peculiar properties about trees, such as the
center of a tree, tree counting, tree coloring. A(x) is one of such properties.
A(x) (accumulation degree of node x) is defined as follows:
- Each edge of the tree has an positive capacity.
- The nodes with degree of one in the tree are named terminals.
- The flow of each edge can't exceed its capacity.
- A(x) is the maximal flow that node x can flow to other terminal nodes.
Since it may be hard to understand the definition, an example is showed below:
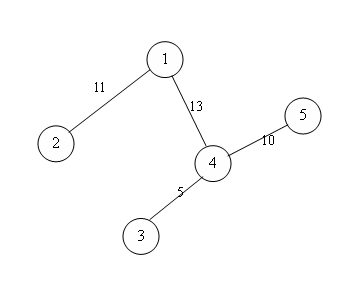
| A(1)=11+5+8=24 |
| Details: |
1->2 |
11 |
| |
1->4->3 |
5 |
| |
1->4->5 |
8(since 1->4 has capacity of 13) |
| A(2)=5+6=11 |
| Details: |
2->1->4->3 |
5 |
| |
2->1->4->5 |
6 |
| A(3)=5 |
| Details: |
3->4->5 |
5 |
| A(4)=11+5+10=26 |
| Details: |
4->1->2 |
11 |
| |
4->3 |
5 |
| |
4->5 |
10 |
| A(5)=10 |
| Details: |
5->4->1->2 |
10 |
The
accumulation degree of a tree is the maximal accumulation degree among
its nodes. Here your task is to find the accumulation degree of the
given trees.
Input
The first line of the input is an integer T which indicates the number of test cases. The first line of each test case is a positive integer n. Each of the following n - 1 lines contains three integers x, y, z separated by spaces, representing there is an edge between node x and node y, and the capacity of the edge is z. Nodes are numbered from 1 to n.
All the elements are nonnegative integers no more than 200000. You may assume that the test data are all tree metrics.
Output
For each test case, output the result on a single line.
Sample Input
1
5
1 2 11
1 4 13
3 4 5
4 5 10
Sample Output
26
Source
这道题的基本思想是树形DP,如果不能理解的话请试图把双向边看成两个单向边,再比划比划就出来了。
当然不一定非要以边做为DP的单元,也可以归到边上(如果你有那份心的话)。
比赛的时候因为数据量大而Stack Overflow,一直想写人工模拟栈,但因为没写过,在比赛中写不出来。
五一节虚心的跟alpc62学习了怎么写人工模拟栈,核心思想就是将同一个DFS内的不同DFS做个标记,这样在出栈的时候就可以判断自己所处的位置,也就知道自己该采取什么行动了。
比如
void DFS(int x) {
for(int i = 0; i < head[x].size(); ++i) {
DFS(head[x][i]);
}
}
如果把(x, i)这个2元组压入栈也就知道自己现在所处的地方了。
如果有更多的内部DFS,同样是加对应的标记。
当然,BFS也是一种很好的选择(应该说大多数队伍会选择BFS而不是人工模拟栈)
//Accumulation Degree in BFS
#include <vector>
#include <algorithm>
#include <iostream>
using namespace std;
#define Min(a, b) (a<b?a:b)
#define Max(a, b) (a>b?a:b)
struct Node
{
int x, i, pre;
Node() {}
Node(int xx, int ii, int pp) {x=xx, i = ii, pre=pp;}
};
struct Edge
{
int x, w, dp;
Edge() {}
Edge(int xx, int ww, int dd=0) { x=xx,w=ww,dp=dd;}
};
const int N = 200010;
vector<Edge> e[N];
bool chk[N];
int n, flow[N];
void solve() {
int i, j, k;
vector<Node> Q;
fill(chk, chk + n, 0);
fill(flow, flow + n, 0);
for(i = 0; i < n && e[i].size()!=1; ++i);
int st = 0, end = 0;
chk[i] = 1;
for(j = 0; j < e[i].size(); ++j) {
Q.push_back(Node(i, j, -1));
end++;
chk[e[i][j].x] = 1;
}
while(st < end) {
int x = e[Q[st].x][Q[st].i].x, pre = Q[st].pre;
for(i = 0; i < e[x].size(); ++i) {
if(!chk[e[x][i].x]) {
Q.push_back(Node(x, i, st));
end++;
chk[e[x][i].x] = 1;
}
}
++st;
}
for(i = end-1; i >= 0; --i) {
int x = Q[i].x, pre = Q[i].pre, idx = Q[i].i;
if(e[e[x][idx].x].size() == 1) e[x][idx].dp = e[x][idx].w;
else e[x][idx].dp = Min(e[x][idx].dp, e[x][idx].w);
if(pre == -1) continue;
int prex = Q[pre].x, preidx = Q[pre].i;
e[prex][preidx].dp += e[x][idx].dp;
}
for(i = 0; i < e[Q[0].x].size(); ++i) {
flow[Q[0].x] += e[Q[0].x][i].dp;
}
for(i = 0; i < end; ++i) {
int x = Q[i].x, pre = Q[i].pre, idx = Q[i].i;
int y = e[x][idx].x, xx;
for(xx = 0; xx < e[y].size() && e[y][xx].x != x; ++xx);
if(pre == -1) {
e[y][xx].dp = e[y][xx].w;
}
else {
e[y][xx].dp = Min(e[y][xx].dp, e[y][xx].w);
}
for(j = 0; j < e[y].size(); ++j) {
flow[y] += e[y][j].dp;
}
for(j = 0; j < e[y].size(); ++j) {
int yy = e[y][j].x;
if(yy == x) continue;
for(k = 0; k < e[yy].size() && e[yy][k].x != y; ++k);
e[yy][k].dp = flow[y] - e[y][j].dp;
}
}
int max = 0;
for(i = 0; i < n; ++i)
max = Max(max, flow[i]);
printf("%d\n", max);
}
int main() {
int ntc;
int i;
int x, y, w;
scanf("%d", &ntc);
while(ntc--) {
scanf("%d", &n);
for(i = 0; i < n; ++i) e[i].clear();
for(i = 0; i < n-1; ++i) {
scanf("%d %d %d", &x, &y, &w);
--x; --y;
e[x].push_back(Edge(y, w));
e[y].push_back(Edge(x, w));
}
solve();
}
return 0;
}