http://acm.hdu.edu.cn/showproblem.php?pid=1028之前用dp做了整数分解,这次学了母函数,用母函数更加方便。理解母函数不难,难在模拟多项式相乘。
首先写成母函数,然后根据该母函数表达式模拟多项式乘法。
//母函数整数拆分
#include <iostream>
using namespace std;
const int M=121;
int a[M]; //存储上一次的系数
int b[M]; //存储这次运算完的系数
int main()
{
int n,i,j,k;
while(scanf("%d",&n)!=EOF)
{
for(i=0;i<=n;i++)
{
a[i]=1; //保存上一个表达式的系数,作为上一个表达式的系数
b[i]=0; //保存上一个表达式和这次的表达式相乘后的系数,初始化为0
}
for(i=2;i<=n;i++)//这次的表达式是指第i个表达式,上一个表达式是指前i-1个表达式相乘后的最终表达式
//第i个表达式的增量为i
{ //所谓上一个表达式的结构是a0*x^0+a1*x^1+a2*x^2+a3*x^3+ +aj*x^j+
+aj*x^j+ +an*x^n
+an*x^n
for(j=0;j<=n;j++) //j是上一个表达式的指数
for(k=0;k+j<=n;k+=i)//k是这一次表达式的指数,增量是i
b[j+k]+=a[j]; //相乘的过程
for(j=0;j<=n;j++)
{
a[j]=b[j];//将相乘之后的系数,赋给a数组,作为上一次表达式的系数,为下一个循环用(如果还有的话)
b[j]=0; //每次都要初始化,为了保存下一次的系数
}
}
printf("%d\n",a[n]);
}
return 0;
} 母函数形式:
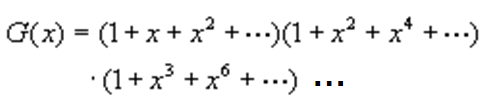
posted on 2011-09-17 14:22
大大木马 阅读(784)
评论(0) 编辑 收藏 引用